4. Trò chơi cũ
Nhiều người trong chúng ta có lẽ đã từng chơi một trò khá “tà đạo” với một đồ thị: Tạo một mảng mới (gọi nó là \(T[i]\)) với \(n\) phần tử. Trong lúc thực hiện duyệt trên đồ thị để tạo ra một đồ thị cây, ta lưu tại chỉ số của các đỉnh này vào mảng \(T\) theo thứ tự thăm đỉnh đó, để từ đó có thể biết được tất cả các nút trong cây con có gốc là một nút \(u\) bất kì trong đồ thị đó chỉ bằng một cặp giá trị \(L_u\), \(R_u\). Có thể nhiều bạn vẫn chưa nhận ra, việc bạn làm đã thể hiện được ý tưởng cơ bản của một thuật toán khác, cũng trong thể loại này, là HLD (hay Heavy-Light Decomposition).
Nói nhiều rồi. Bây giờ, cũng là lúc mà chúng ta thử thực hiện điều ngược lại, cũng cho vui, cũng như cách mà chúng ta đã bắt đầu trick này vậy.
Cho \(n\) đỉnh và \(n - 1\) cạnh ẩn, tạo thành một đồ thị cây. Có tổng cộng \(n\) cặp \(L_i\), \(R_i\), và cặp thứ \(i\) cho biết với mảng \(T\) được tạo ra thông qua quá trình duyệt cây, thì toàn bộ số thứ tự các đỉnh nằm trong đoạn từ \(L_i\) đến \(R_i\) hoặc là số thứ tự đỉnh \(i\), hoặc là số thứ tự của đỉnh con của cây con với gốc là đỉnh \(i\).
Hãy khôi phục lại toàn bộ cây bị ẩn, bằng cách in ra \(n - 1\) cạnh mà bạn cho rằng là đồ thị cây ban đầu. Biết quy tắc duyệt cây được sử dụng trong bài này là như sau (được viết lại bằng ngôn ngữ \(\text{Python 3}\)):
n = int(input())
r = int(input())
graph = []
for loop in range(n + 1):
graph.append([])
T = [0] * (n + 1)
L = [0] * (n + 1)
R = [0] * (n + 1)
timeDfs = 0
def DFS(u: int, p: int):
global timeDfs, T
timeDfs += 1
T[timeDfs] = u
L[u] = timeDfs
for v in graph[u]:
if v == p:
continue
DFS(v, u)
R[u] = timeDfs
for i in range(n - 1):
u, v = [int(x) for x in input().split()]
graph[u].append(v)
graph[v].append(u)
DFS(r, 0)
for i in range(n):
print(L[i + 1], R[i + 1]) #your input here
\(\text{Input}\) [oldtrick.inp]
- Dòng một gồm một số \(n\) \((2 \le n \le 5*10^5)\), thể hiện số lượng đỉnh của cây cho trước.
- \(n\) dòng sau, dòng thứ \(i\) gồm một cặp chỉ số \(L_i\), \(R_i\) \((1 \le L_i, R_i \le n)\), thể hiện rằng với các tạo ra mảng \(T\) theo như mô tả ở trên đề, các số trong đoạn từ \(L_i\) đến \(R_i\) sẽ là hoặc chỉ số của đỉnh \(i\) hoặc chỉ số của đỉnh con của đỉnh có số thứ tự là \(i\) trong cây cho trước.
- \(\text{Input}\) trong tất cả các test được đảm bảo có ít nhất một cách biểu diễn cây thỏa mãn đề bài phù hợp với dữ liệu được cho.
\(\text{Output}\) [oldtrick.out] #Multiple_Answers
Cần in ra \(n\) dòng, trong đó:
- Dòng đầu tiên in ra số thứ tự \(r\) gốc của cây ban đầu \((1 \le r \le n)\).
- \(n - 1\) dòng tiếp theo, mỗi dòng gồm hai số \(u_i\), \(v_i\) \((1 \le u_i, v_i \le n)\), thể hiện rằng có một cạnh vô hướng nối giữa đỉnh có số thứ tự là \(u_i\) và đỉnh có số thứ tự là \(v_i\).
\(\text{Scoring}\)
- Subtask \(0\) \((3\%)\): Example tests.
- Subtask \(1\) \((15\%)\): Gọi gốc của cây ban đầu là \(r\). Với mọi \(i \ne r\), \(L_i = R_i\);
- Subtask \(2\) \((10\%)\): \(R_i = n\), tập hợp các giá trị \(L_i\) tạo thành một hoán vị của các số từ \(1\) đến \(n\).
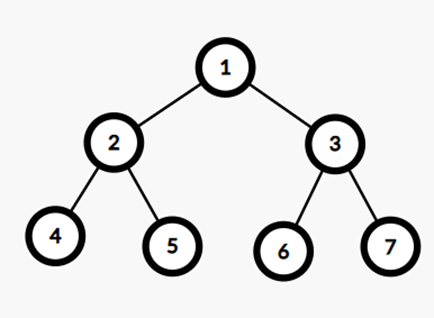
- Subtask \(3\) \((10\%)\): Cây ban đầu (được ẩn) có dạng cây nhị phân (với \(n = 2^k - 1\), với \(k \in \mathbb{N}\), \(k > 0\)). Xem \(\text{Example Test 2}\) để biết hình dạng của cây nhị phân.
- Subtask \(4\) \((27\%)\): \(n ≤ 2000\).
- Subtask \(5\) \((25\%)\): \(n ≤ 10^5\).
- Subtask \(6\) \((10\%)\): Full.
\(\text{Example Tests}\)
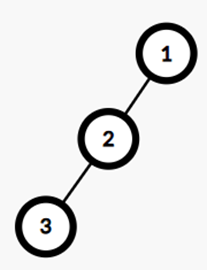
\(\text{Example Test 1}\)
\(\text{Input}\)
3
1 3
2 3
3 3
\(\text{Output}\)
1
1 2
2 3
\(\text{Explanation}\)
\(\text{Example Test 2}\)
\(\text{Input}\)
7
1 7
2 4
5 7
3 3
4 4
6 6
7 7
\(\text{Output}\)
1
1 2
1 3
2 4
2 5
3 6
3 7
\(\text{Explanation}\)
\(\text{Example Test 3}\)
\(\text{Input}\)
7
1 7
2 6
7 7
3 5
6 6
4 4
5 5
\(\text{Output}\)
1
1 2
1 3
2 4
2 5
4 6
4 7
\(\text{Explanation}\)
