LQDOJ CUP 2023 - Round 6

Cứ vào mùa hè hằng năm, trường chuyên Đ sẽ tổ chức một buổi giao lưu ngoại khóa giữa các trường trong thành phố, và các trò chơi đồng đội là thứ không thể nào thiếu. Có \(n\) học sinh đến từ \(m\) trường khác nhau sẽ tham gia các trò chơi năm nay. Các học sinh sẽ đứng xếp hàng theo thứ tự đánh số từ \(1\) tới \(n\). Ban tổ chức dự định sẽ chia các học sinh thành một số đội từ \(n\) học sinh, mỗi học sinh thuộc đúng duy nhất một đội và một đội phải có tối thiểu một học sinh.

Để cho đơn giản, họ sẽ tách hàng đang đứng hiện tại thành một hoặc một số hàng liên tiếp và mỗi hàng sau khi tách như thế sẽ là một đội. Tuy nhiên, một đội không thể có học sinh thuộc quá nhiều trường khác nhau, bởi như thế thì các thầy cô sẽ rất khó quản lý. Mặt khác, một đội cũng không thể có học sinh thuộc quá ít trường khác nhau, bởi khi đó thì các bạn sẽ chỉ chơi với những người cùng trường, gây chia rẽ nội bộ và gây khó khăn cho các học sinh trong việc làm quen với những bạn mới trong đội mình. Sau khi cân nhắc kỹ càng, ban tổ chức quyết định một đội sẽ có các thành viên thuộc tối thiểu \(l\) trường khác nhau và tối đa \(r\) trường khác nhau.

Tuy ràng buộc phức tạp như vậy, nhưng vẫn có rất nhiều cách khác nhau để xếp đội, vì vậy bạn hãy giúp ban tổ chức tính số cách xếp đội khác nhau nhé. Lưu ý là có thể xếp thành một đội duy nhất gồm cả \(n\) thí sinh.

Input

• Dòng đầu tiên chứa số nguyên \(t\) \((1 \leq t \leq 10)\) là số lượng trường hợp. Mỗi trường hợp gồm:
  • Dòng đầu tiên chứa bốn số nguyên \(n\), \(m\), \(l\) và \(r\) \((1 \leq l \leq r \leq m \leq n \leq 180504)\), lần lượt là số học sinh tham gia, số trường, và hai số \(l\), \(r\) như mô tả của đề.
  • Dòng tiếp theo chứa \(n\) số nguyên \(a_1, a_2, \ldots, a_n\) \((1 \leq a_i \leq m)\), với \(a_i\) là trường của học sinh thứ \(i\).

Output

• Gồm \(t\) dòng, mỗi dòng chứa một số nguyên duy nhất là số cách xếp đội của trường hợp tương ứng. Vì kết quả có thể rất lớn, hãy in phần dư của kết quả khi chia cho \(918052004\).

Scoring

• Subtask \(1\) (\(30\%\) số điểm): \(n \leq 15\).
• Subtask \(2\) (\(20\%\) số điểm): \(n \leq 185\).
• Subtask \(3\) (\(20\%\) số điểm): \(n \leq 1805\).
• Subtask \(4\) (\(30\%\) số điểm): Không có ràng buộc gì thêm.

Example

3
6 6 1 1
1 2 3 4 5 6
6 6 6 6
1 2 3 4 5 6
9 4 2 3
1 2 4 3 2 2 1 3 4

1
1
6

Bạn được cho một cây nhị phân gồm \(n\) đỉnh có gốc là đỉnh \(s\) sao cho mỗi đỉnh có đúng \(0\) hoặc \(2\) đỉnh con. Bạn được phép thực hiện thao tác sau đây với số lần tuỳ ý: chọn một đỉnh có hai đỉnh con và đảo vị trí của hai cây con có gốc là hai đỉnh con đó.

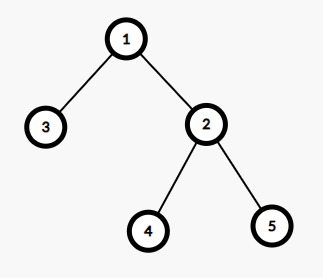
Ví dụ, cho một cây nhị phân gồm \(5\) đỉnh có gốc là đỉnh \(1\), thực hiện thao tác chọn đỉnh \(1\) và đảo vị trí của cây con gốc \(2\) và cây con gốc \(3\):

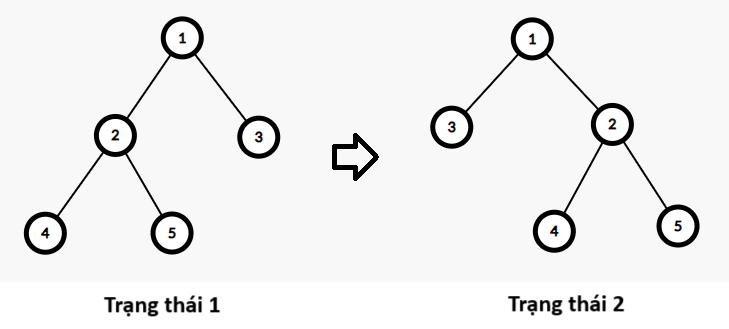
Tiếp tục thực hiện thao tác chọn đỉnh \(2\) và đảo vị trí của cây con gốc \(4\) và cây con gốc \(5\):

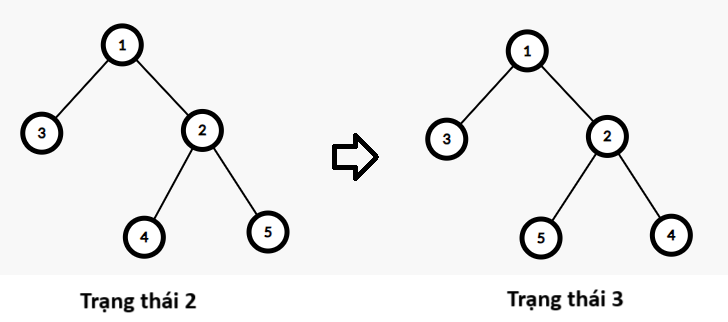
Hãy tìm cách thực hiện thao tác sao cho số lượng cặp nghịch thế trong dãy được tạo ra từ thứ tự duyệt trước (Pre-order Traversal) của cây nhận được sau cùng là nhỏ nhất, biết rằng số lượng cặp nghịch thế của một dãy \(a_1, a_2, \ldots, a_m\) là số lượng cặp vị trí \((i, j)\) thoả mãn \(1 \leq i < j \leq m\) và \(a_i > a_j\). Ví dụ, dãy thứ tự duyệt trước của cây trạng thái \(1\) là \(\{1, 2, 4, 5, 3\}\) có \(2\) cặp nghịch thế, dãy thứ tự duyệt trước của cây trạng thái \(2\) là \(\{1, 3, 2, 4, 5\}\) có \(1\) cặp nghịch thế, dãy thứ tự duyệt trước của cây trạng thái \(3\) là \(\{1, 3, 2, 5, 4\}\) có \(2\) cặp nghịch thế.

Input

• Dòng đầu tiên chứa hai số nguyên \(n\) và \(s\) \((1 \leq s \leq n \leq 2 \times 10^5)\) là số lượng đỉnh của cây và đỉnh gốc của cây.
• Trong \(n-1\) dòng tiếp theo, mỗi dòng chứa hai số nguyên \(u\) và \(v\) \((1 \leq u, v \leq n)\) mô tả một cạnh của cây.

Output

• Một số nguyên duy nhất là số cặp nghịch thế nhỏ nhất theo yêu cầu bài toán.

Scoring

• Subtask \(1\) (\(15\%\) số điểm): \(n \leq 16\).
• Subtask \(2\) (\(40\%\) số điểm): \(n \leq 5 \times 10^3\).
• Subtask \(3\) (\(25\%\) số điểm): Đỉnh cha của đỉnh \(u\) \((2 \leq u \leq n)\) là đỉnh \(\left\lfloor \frac{u}{2} \right\rfloor\).
• Subtask \(4\) (\(20\%\) số điểm): Không có ràng buộc gì thêm.

Example

Test 1

Input

5 1
1 2
5 2
2 4
3 1

Output

1

Note

Cây được biến đổi thành dạng như sau:

Dãy thứ tự duyệt trước là \(\{1, 3, 2, 4, 5\}\) có đúng \(1\) cặp nghịch thế là kết quả tối ưu.

7 3
2 4
6 7
1 6
6 3
3 4
4 5

7

Hôm nay bé Si làm bánh, mời những người bạn tới nhà để ăn mừng chức vô địch World Cup. Trên mặt phẳng tọa độ, chiếc bánh của bé Si được xem như là một đa giác điểm nguyên không tự cắt. Bé Rô - người bạn thân nhất của bé Si cũng tới nhà Si để ăn mừng thành tích của bạn mình.

Lúc này Rô nghĩ ra một thử thách để làm khó Si. Rô đưa ra \(q\) câu hỏi, với mỗi câu hỏi Rô sẽ đưa ra hai số nguyên \(l\) và \(r\), khi đó Rô sẽ dùng dao để cắt toàn bộ phần bánh bị giới hạn bởi hai đường thẳng \(x = l\) và \(x = r\) (có thể là không có phần bánh nào). Với mỗi câu hỏi như thế, Rô đố Si hãy tính diện tích phần bánh bị cắt ra. Lưu ý rằng mỗi câu hỏi được xem như một trường hợp riêng biệt và không ảnh hưởng đến nhau.

Input

• Dòng đầu tiên chứa hai số nguyên \(n\) và \(q\) \((3 \leq n \leq 2 \times 10^5, 1 \leq q \leq 2 \times 10^5)\) là số đỉnh của đa giác và số truy vấn.
• Trong \(n\) dòng tiếp theo, dòng thứ \(i\) chứa hai số nguyên \(x_i\) và \(y_i\) \((|x_i|, |y_i| \leq 10^9)\) là toạ độ của đỉnh thứ \(i\). Điểm \((x_i, y_i)\) có cạnh nối tới đỉnh \((x_{i+1}, y_{i+1})\) với \(1 \le i < n\) và đỉnh \((x_n, y_n)\) có cạnh nối tới đỉnh \((x_1, y_1)\). Dữ liệu đảm bảo các đỉnh được cho lần lượt theo chiều kim đồng hồ.
• Trong \(q\) dòng tiếp theo, mỗi dòng chứa hai số nguyên \(l\) và \(r\) \((-10^9 \leq l \leq r \leq 10^9)\) mô tả một truy vấn.

Output

• Gồm \(q\) dòng, mỗi dòng chứa một số thực là diện tích phần bánh bị cắt ra ứng với mỗi truy vấn.
• Đáp án của bạn được chấp nhận nếu chênh lệch tương đối không vượt quá \(10^{-6}\). Hay nói cách khác, nếu đáp án của bạn là \(a\) và đáp án của giám khảo là \(b\), đáp án của bạn được chấp nhận nếu \(\frac{|a - b|}{\max(1, b)} \leq 10^{-6}\).

Scoring

• Subtask \(1\) (\(15\%\) số điểm): \(n \le 10^3\), \(|x_i|, |y_i| \leq 5 \times 10^4\) và bánh luôn có dạng đa giác lồi.
• Subtask \(2\) (\(15\%\) số điểm): \(n \le 10^3\), \(|x_i|, |y_i| \leq 5 \times 10^4\) và các cạnh của bánh luôn song song với trục tọa độ.
• Subtask \(3\) (\(20\%\) số điểm): \(n \le 10^3\), \(|x_i|, |y_i| \leq 5 \times 10^4\).
• Subtask \(4\) (\(15\%\) số điểm): Bánh luôn có dạng đa giác lồi.
• Subtask \(5\) (\(15\%\) số điểm): Các cạnh của bánh luôn song song với trục tọa độ.
• Subtask \(6\) (\(20\%\) số điểm): Không có ràng buộc gì thêm.

Example

Test 1

Input

8 3
3 3
3 0
-2 0
-2 1
0 1
0 3
-2 3
0 6
-2 3
0 3
-3 0

Output

18.5
13.5
5.0

Note

Đây là hình minh họa: