LQDOJ CUP 2023 - Round 5

Cậu bé Mika là một người rất thích đi du lịch cũng giao lưu với những người bạn từ nhiều nơi. Trên mạng xã hội, Mika đã làm quen được \(n\) người bạn và họ sinh sống tại \(n\) thành phố khác nhau trên đất nước. Các thành phố được đánh số từ \(1\) đến \(n\) và được nối với nhau thông qua \(n - 1\) con đường hai chiều sao cho có thể đến được mỗi thành phố từ bất kỳ thành phố nào khác bằng cách đi qua một số con đường, con đường thứ \(i\) kết nối trực tiếp hai thành phố \(a_i\) và \(b_i\).

Vào ngày cuối tuần, Mika quyết định đi đến thăm tất cả những người bạn mới này. Hiện tại, Mika đang ở thành phố thứ nhất và thăm được người bạn đầu tiên. Sau đó anh ấy quyết định thứ thăm người bạn sống ở thành phố thứ \(2\), rồi mới thăm đến người bạn sống ở thành phố thứ \(3\), ... cuối cùng là người bạn sống ở thành phố thứ \(n\). Để đi qua một con đường nhất định, Mika cần phải có một vé hợp lệ. Con đường thứ \(i\) có thể được đi qua nếu bạn có vé một lượt giá \(c_{i_1}\) đồng hoặc vé nhiều lượt giá \(c_{i_2}\) đồng. Vé một lượt chỉ cho phép đi qua con đường một lần, còn vé nhiều lượt thì không giới hạn số lần đi qua con đường đó. Mika muốn tiết kiệm chi phí di chuyển nên hãy giúp cậu ấy tính toán chi phí tối thiểu để Mika có thể đi thăm tất cả người bạn của mình.

Input

• Dòng đầu tiên chứa số nguyên \(n\) \((2 \leq n \leq 2 \times 10^5)\) là số lượng thành phố.
• Trong \(n - 1\) dòng tiếp theo, dòng thứ \(i\) chứa bốn số nguyên \(a_i, b_i, c_{i_1}, c_{i_2}\) \((1 \leq a_i,b_i \leq n, 1 \leq c_{i_1}, c_{i_2} \leq 10^5)\) mô tả một con đường.

Output

• Một số nguyên duy nhất là chi phí tối thiểu để Mika có thể đi thăm tất cả người bạn của mình.

Scoring

• Subtask \(1\) (\(20\%\) số điểm): \(c_{i_1} = c_{i_2}\) với mọi \(1 \leq i \leq n - 1\).
• Subtask \(2\) (\(20\%\) số điểm): \(n \leq 2 \times 10^3\).
• Subtask \(3\) (\(20\%\) số điểm): Mỗi thành phố kết nối trực tiếp với tối đa hai thành phố khác.
• Subtask \(4\) (\(20\%\) số điểm): Các thành phố và các con đường tạo thành một cây nhị phân hoàn hảo với đỉnh \(1\) là gốc.
• Subtask \(5\) (\(20\%\) số điểm): Không có ràng buộc gì thêm.

Example

4
1 2 3 5
1 3 2 4
2 4 1 3

10

4
1 4 5 5
3 4 4 7
2 4 2 6

16

5
1 2 2 3
1 3 2 3
1 4 2 3
1 5 2 3

11

Rumiru là một cô bé rất thích chơi với slime. Hôm nay, cô quyết định đến một cửa hàng để mua một số con về chơi. Trong cửa hàng có trưng bày \(n\) con slime, con thứ \(i\) từ trái sang phải có kích thước \(a_i\). Rumiru muốn mua một số con slime và gộp một số cặp lại với nhau để tạo thành ít nhất một con có kích thước đúng bằng \(s\), quy tắc gộp như sau:

• Chọn hai con slime bất kỳ có kích thước bằng nhau và gộp chúng lại thành một con mới có kích thước bằng tổng kích thước của hai con cũ.

Hãy giúp Rumiru đếm số cách mua thoả mãn điều kiện. Biết rằng, hai cách mua được xem là khác nhau khi tồn tại một con slime được mua ở cách này nhưng không được mua ở cách còn lại.

Input

• Dòng đầu tiên chứa hai số nguyên \(n\) và \(s\) \((1 \leq n \leq 2 \times 10^5, 1 \leq s \leq 5 \times 10^3)\) lần lượt là số lượng con slime và kích thước slime mong muốn.
• Dòng tiếp theo chứa \(n\) số nguyên \(a_1, a_2, \ldots, a_n\) (\(1 \leq a_i \leq s\)) là kích thước của các con slime.

Output

• Một số nguyên duy nhất là phần dư số cách mua khi chia cho \(10^9 + 7\).

Scoring

• Subtask \(1\) (\(20\%\) số điểm): \(n \leq 20\).
• Subtask \(2\) (\(30\%\) số điểm): \(n \leq 2 \times 10^3\).
• Subtask \(3\) (\(10\%\) số điểm): \(a_1 = a_2 = \ldots = a_n\).
• Subtask \(4\) (\(40\%\) số điểm): Không có ràng buộc gì thêm.

Example

3 2
1 1 2

5

5 4
1 1 2 3 4

18

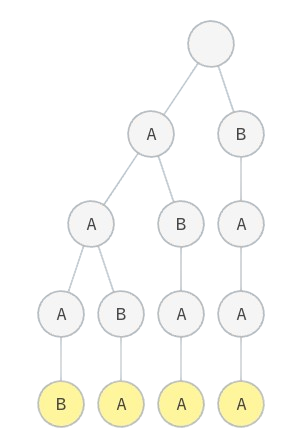
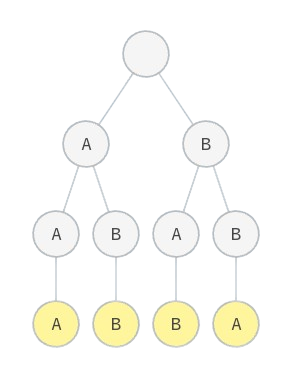
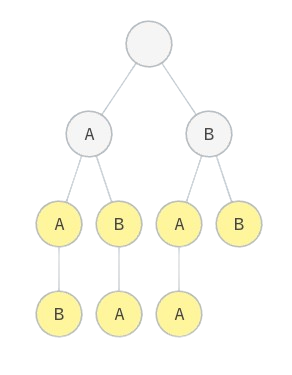
Cho tập hợp \(S\) gồm \(n\) xâu kí tự: \(S_1, S_2, \dots, S_n\). Kí tự trong các xâu này có thể là a hoặc b.

Một xâu \(A\) được gọi là xâu hoán vị của xâu \(B\), nếu ta có thể tạo ra được xâu \(A\) bằng cách sắp xếp lại các kí tự của xâu \(B\). Hãy tạo tập hợp \(S'\) theo nguyên tắc sau: với mỗi xâu \(S_i\) \((1 \le i \le n)\), ta thêm tất cả các xâu hoán vị của \(S_i\) vào \(S'\). Nói cách khác, \(S'\) là tập hợp các xâu hoán vị của \(n\) xâu thuộc \(S\).

Ta tiến hành dựng cây trie của tập xâu \(S'\) vừa tạo. Hãy cho biết cây trie này có bao nhiêu nút.

Nhắc lại về Trie

Trie là một cấu trúc dữ liệu dạng cây dùng để lưu trữ một danh sách các xâu với bộ kí tự hữu hạn, cho phép việc lưu trữ các xâu hiệu quả có tiền tố giống nhau.

Cây trie được dựng theo nguyên tắc: mỗi nút liên kết với một xâu ký tự sao cho các xâu ký tự của tất cả các nút con của một nút đều có chung một tiền tố, chính là xâu ký tự của nút đó. Nút gốc tương ứng với xâu ký tự rỗng.

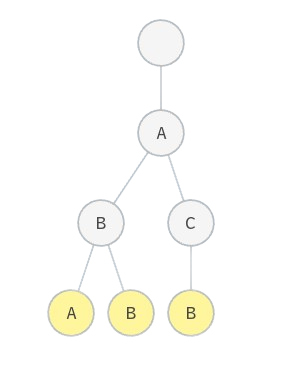
Ví dụ, với các xâu aba, abb, acb, ta dựng được một cây trie gồm \(7\) nút như sau:

Input

• Dòng đầu tiên chứa số nguyên \(n\) \((1 \leq n \leq 20)\) là số lượng xâu trong tập \(S\).
• Trong \(n\) dòng tiếp theo, dòng thứ \(i\) chứa xâu \(S_i\) \((1 \le |S_i| \le 10^5)\), các kí tự của xâu chỉ có thể là a hoặc b.

Output

• In ra một số nguyên duy nhất là phần dư của đáp án bài toán khi chia cho \(10^9+7\).

Scoring

• Subtask \(1\) (\(20\%\) số điểm): \(|S_i| \leq 20\).
• Subtask \(2\) (\(20\%\) số điểm): \(n = 1, |S_i| \leq 10^3\).
• Subtask \(3\) (\(15\%\) số điểm): \(n = 2, |S_i| \leq 10^3\).
• Subtask \(4\) (\(10\%\) số điểm): \(|S_i| \leq 10^3\).
• Subtask \(5\) (\(15\%\) số điểm): \(n = 1\).
• Subtask \(6\) (\(10\%\) số điểm): \(n = 2\).
• Subtask \(7\) (\(10\%\) số điểm): Không có ràng buộc gì thêm.

Example

Test 1

Input

1
abaa

Output

14

Note

Với xâu abaa, ta tạo được các xâu hoán vị tương ứng như sau:

1. aaab
2. aaba
3. abaa
4. baaa

Từ đây, ta dựng được cây trie gồm \(14\) nút.

Test 2

Input

2
abb
aaa

Output

11

Note

Với mỗi xâu trong tập \(S\), ta tạo được các xâu hoán vị tương ứng như sau:

• abb \(\to\) abb, bab, bba
• aaa \(\to\) aaa

Từ đây, ta dựng được cây trie gồm \(11\) nút.

Test 3

Input

4
aa
ab
bb
aba

Output

10

Note

Với mỗi xâu trong tập \(S\), ta tạo được các xâu hoán vị tương ứng như sau:

• aa \(\to\) aa
• ab \(\to\) ab, ba
• bb \(\to\) bb
• aba \(\to\) aba, aab, baa

Từ đây, ta dựng được cây trie gồm \(10\) nút.