3. LQDOJ CUP 2022 - Final Round - TRINET
Trước đêm 30 Tết, gia đình Mai bận rộn chuẩn bị rất nhiều thứ để đón năm mới, chỉ có Mai là không có việc gì làm, vì vậy cô đã rủ bạn bè chơi nhảy lò cò. Vì Mai đã chơi trò này rất nhiều lần nên cô muốn thay đổi cho thú vị hơn. Trò chơi mới như sau, trên mặt sân vẽ một lưới tam giác có \(n\) hàng như hình sau:
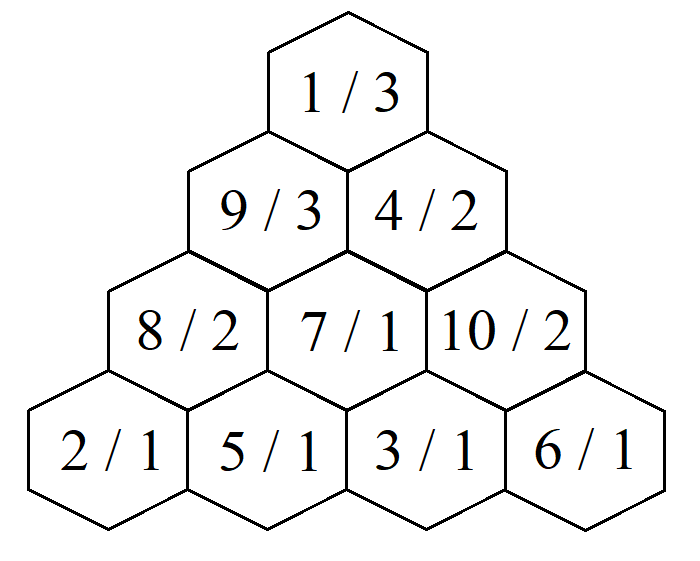
Hàng thứ \(i\) sẽ có \(i\) ô. Gọi ô \((i, j)\) là ô thứ \(j\) của hàng \(i\). Mỗi ô \((i, j)\) được viết hai số có dạng "\(A_{i,j} \, / \, B_{i,j}\)" với:
- \(A_{i,j}\) là giá trị của ô (tất cả các ô có giá trị đôi một khác nhau) và,
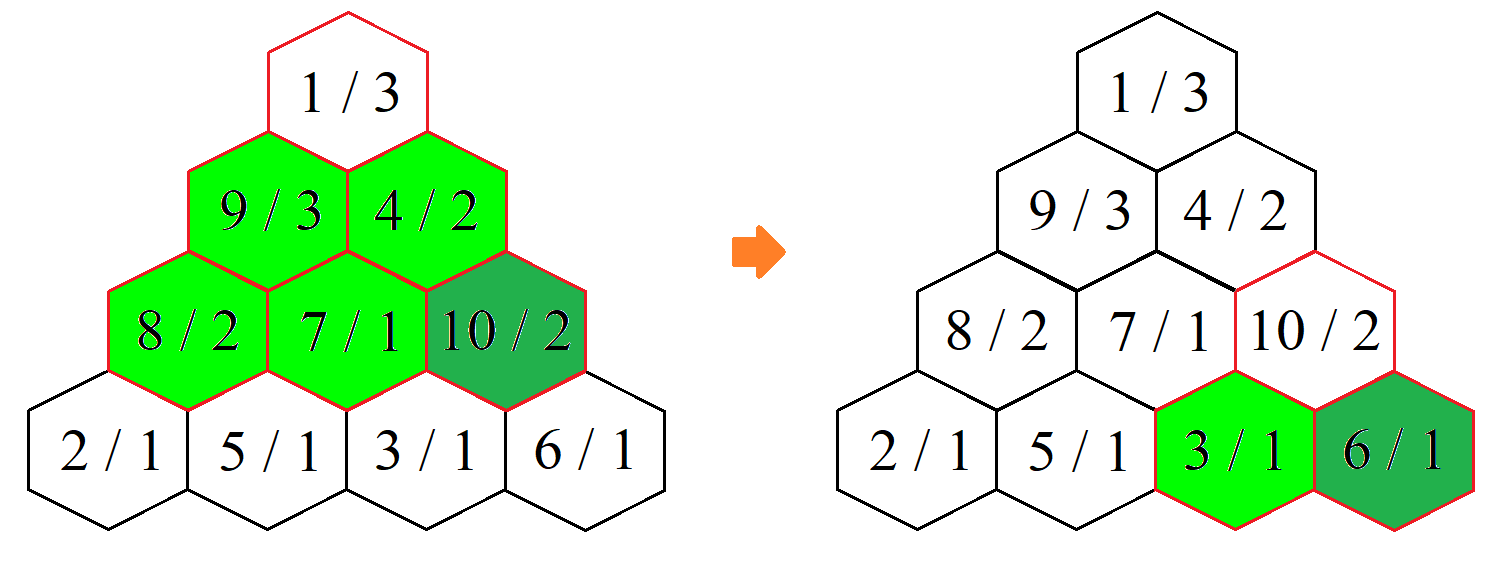
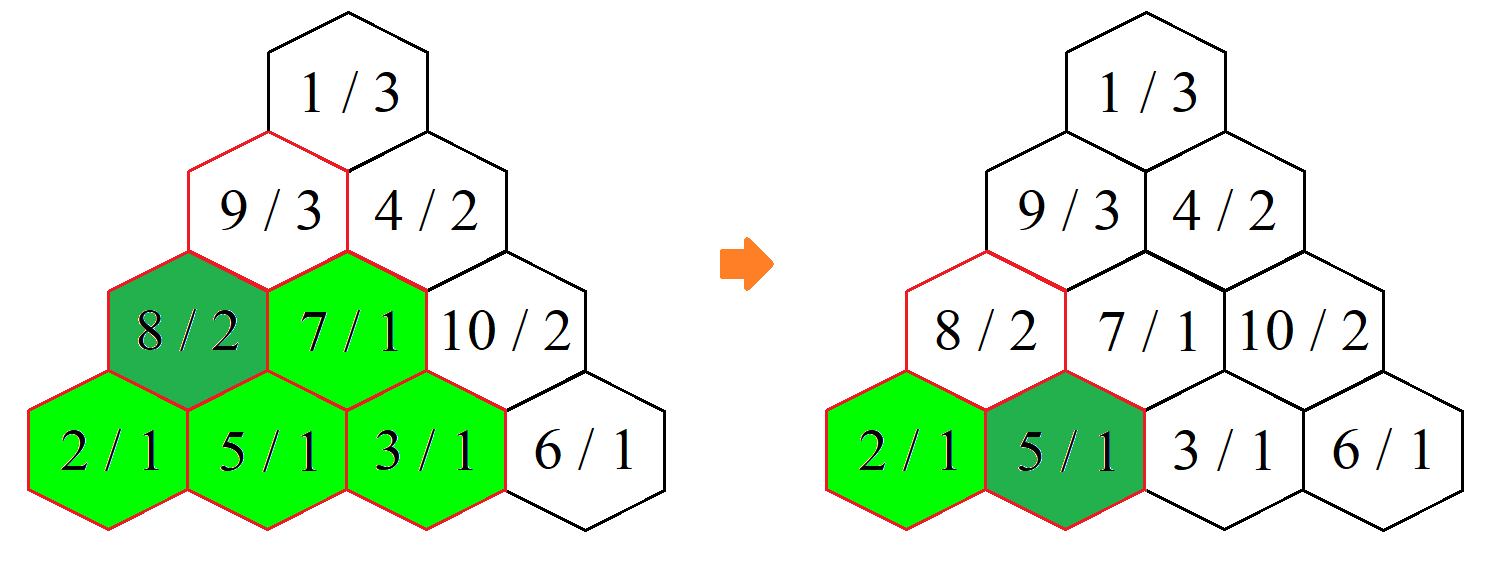
- \(B_{i,j}\) là giới hạn nhảy của ô, nghĩa là khi người chơi đứng ở ô \((i,j)\), người đó chỉ có thể nhảy đến những ô khác ô \((i,j)\) nằm trong tam giác đều có kích thước \(B_{i,j}\) với đỉnh trên cùng là ô \((i,j)\).
Ở mỗi lần chơi, người chơi sẽ xuất phát từ một ô bất kỳ, có thể nhảy nhiều lượt, mỗi lượt được nhảy đến một ô trong giới hạn nhảy. Lần chơi kết thúc khi người đó không thể nhảy đến ô nào nữa. Điểm của lần chơi đó là tổng giá trị các ô mà người chơi đã chạm vào.
Mai quyết định mỗi lần chơi sẽ xuất phát ở một ô khác nhau, mỗi ô đúng một lần, và mỗi lượt nhảy cô luôn nhảy đến ô có giá trị cao nhất trong tất cả các ô có thể nhảy đến. Mai muốn thử hết xuất phát từ tất cả các ô, mỗi lần một ô khác nhau, và muốn biết điểm sau mỗi lần chơi là bao nhiêu.
Yêu cầu: Bạn hãy giúp Mai tính điểm nhận được sau mỗi lần chơi là bao nhiêu. Vì kết quả có thể rất lớn, nên bạn hãy in kết quả theo phép tính sau:
Trong đó:
- \(a \oplus b\) là phép XOR hai số nguyên \(a\) và \(b\), trong ngôn ngữ C++ phép tính XOR là
^, trong ngôn ngữ Pascal phép tính XOR làxor. - \(\texttt{score}_{i,j}\) là điểm nhận được của lần chơi xuất phát từ ô \((i,j)\).
Input
- Dòng đầu tiên chứa số nguyên \(n\) \((1 \leq n \leq 2000)\) là số hàng của lưới tam giác.
- Vì input khá lớn nên input của một cặp số \(A_{i, j}, B_{i, j}\) sẽ có số \(D_{i, j} = A_{i, j}\cdot 5000 + B_{i, j}\) \((1 \leq A_{i,j} \leq 10^7, 1 \leq B_{i,j} \leq n - i + 1)\)
- Dòng thứ \(i\) trong số \(n\) dòng tiếp theo chứa \(i\) số nguyên \(D_{i,j} (1 \leq j \leq i)\) là giá trị của cặp số như được miêu tả ở trên.
Output
- Ghi ra một dòng duy nhất chứa một số nguyên là kết quả của bài toán.
Scoring
- Subtask \(1\) (\(20\%\) số điểm): \(B_{i,j} \leq 2\) với mọi \((i, j)\).
- Subtask \(2\) (\(20\%\) số điểm): Các ô ở hàng dưới luôn có giá trị cao hơn các ô ở hàng trên.
- Subtask \(3\) (\(20\%\) số điểm): \(n \leq 500\).
- Subtask \(4\) (\(40\%\) số điểm): Không có ràng buộc gì thêm.
Example
Test 1
Input
4
5003
45003 20002
40002 35001 50002
10001 25001 15001 30001Output
111Note
Xét lần chơi xuất phát từ ô \((1,1)\):
Mai nhảy từ ô \((1,1)\) đến ô \((3,3)\) và kết thúc ở ô \((4,4)\). Điểm nhận được là \(1 + 10 + 6 = 17\).
Xét lần chơi xuất phát từ ô \((2,1)\):
Mai nhảy từ ô \((2,1)\) đến ô \((3,1)\) và kết thúc ở ô \((4,2)\). Điểm nhận được là \(9 + 8 + 5 = 22\).