LQDOJ contest #12

Số \(\pi\) viết đến chữ số thập phân thứ \(100\) là

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679.

Tức là, cắt ngắn số \(\pi\) trên để nó có đúng \(n\) chữ số thập phân.

Input

• Chứa duy nhất một số nguyên dương \(n ~ (1 \leq n \leq 100)\).

Output

• In ra số \(\pi\) được viết đến chữ số thập phân thứ \(n\) trên một dòng duy nhất.

2

3.14

32

3.14159265358979323846264338327950

100

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679

Cho một số nguyên dương \(n ~ (1 \leq n \leq {10}^{12})\), hãy đếm số bộ số nguyên dương \((x, y)\) thỏa mãn các điều kiện sau:

• \(x > 0\) và \(y > 0\),
• \(x \times \lfloor \sqrt{y} \rfloor + y = n\).

Trong đó \(\lfloor x \rfloor\) là số nguyên lớn nhất không vượt quá \(x\).

Input

• Một dòng duy nhất chứa số nguyên dương \(n\).

Output

• Chứa duy nhất một số nguyên tương ứng với số bộ số \((x, y)\) thỏa mãn.

Scoring

• Subtask 1 (\(10\%\) số điểm): \(n \leq 20\).
• Subtask 2 (\(20\%\) số điểm): \(n \leq 1000\).
• Subtask 3 (\(30\%\) số điểm): \(n \leq {10}^6\).
• Subtask 4 (\(40\%\) số điểm): \(n \leq {10}^{12}\).

2

1

3

2

Ở một vũ trụ nào đó, Đường Tăng lên Tây Trúc thỉnh kinh nhưng không đi cùng Ngộ Không, Bát Giới và Sa Tăng. Do trên đường đi có thể gặp nhiều yêu quái nên Đường Tăng muốn lập tổ đội gồm nhiều người. Để có thể đảm bảo an toàn, Đường Tăng đã mở hội chọn người đồng hành. Hội này có tổng cộng \(n\) người đến ứng tuyển, vì mỗi người đều muốn đảm bảo an toàn cho bản thân nên người thứ \(i\) đến tham gia sẽ yêu cầu trong đội có ít nhất \(a_i\) thành viên (tính cả Đường Tăng và người thứ \(i\)). Do có tài ăn nói nên Đường Tăng có thể thuyết phục người thứ \(i\) vào đội trong trường hợp ông có thể đảm bảo về số lượng thành viên trong đội. Đường tăng cần chọn một số người để lập ra đội thỉnh kinh, sao cho "điều kiện an toàn" của tất cả các thành viên đều thỏa mãn.

Yêu cầu: Hãy tìm số lượng thành viên lớn nhất mà đội thỉnh kinh này có thể có được (tính cả Đường Tăng).

Input

• Dòng đầu tiên gồm một số nguyên dương \(n ~ (1 \leq n \leq 7\times {10}^6)\) là số người ứng tuyển vào đội thỉnh kinh.
• Dòng thứ hai gồm \(n\) số nguyên \(a_1, a_2, \ldots, a_n ~ (1 \leq a_i \leq {10}^9)\), trong đó \(a_i\) thể hiện điều kiện gia nhập đội thỉnh kinh của người thứ \(i\).

Output

Gồm một số nguyên duy nhất là số lượng thành viên lớn nhất có thể của đội thỉnh kinh.

Scoring

• Subtask 1 (\(10\%\) số điểm): \(n \leq 20\).
• Subtask 2 (\(40\%\) số điểm): \(n \leq {10}^5\).
• Subtask 3 (\(50\%\) số điểm): Không có ràng buộc gì thêm.

6
2 1 1 3 7 8

5

5
3 4 5 6 7

1

8
8 4 11 6 7 2 6 2

8

Cho một đa giác đều gồm \(n ~ (3 \leq n \leq {10}^9)\) đỉnh, các cạnh có độ dài là \(1\), các đỉnh được đánh số từ \(1\) đến \(n\) theo chiều ngược chiều kim đồng hồ. Một tam giác có thể được tạo thành từ \(3\) đỉnh \(i, j, k ~ (1 \leq i < j < k \leq n)\) phân biệt của đa giác. Tam giác có ba đỉnh \(i, j, k\) được kí hiệu là \(\triangle ijk\).

Hai tam giác \(\triangle ijk\) và \(\triangle i'j'k'\) được gọi là bằng nhau khi và chỉ khi các cạnh \(ij, jk, ik\) và \(i'j', j'k', i'k'\) có thể tạo thành \(3\) cặp cạnh, mỗi cặp có hai cạnh có độ dài bằng nhau, mỗi cạnh trong \(6\) cạnh kia thuộc đúng một cặp và mỗi cặp gồm một cạnh của \(\triangle ijk\) và một cạnh của \(\triangle i'j'k'\).

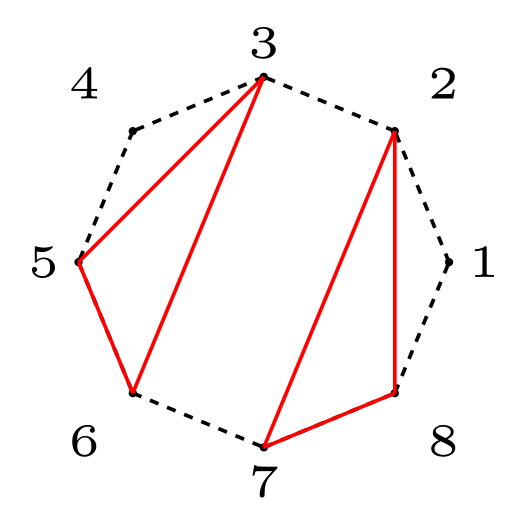
Trong trường hợp đầu tiên, tam giác \(\triangle 278\) bằng \(\triangle 356\) bởi vì

• cạnh 2-8 bằng cạnh 3-5,
• cạnh 2-7 bằng cạnh 3-6,
• cạnh 5-6 bằng cạnh 7-8.

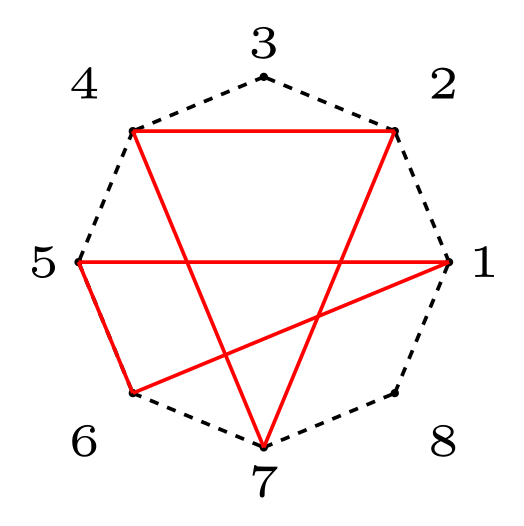
Trong trường hợp thứ hai, hai tam giác đã cho bằng nhau.

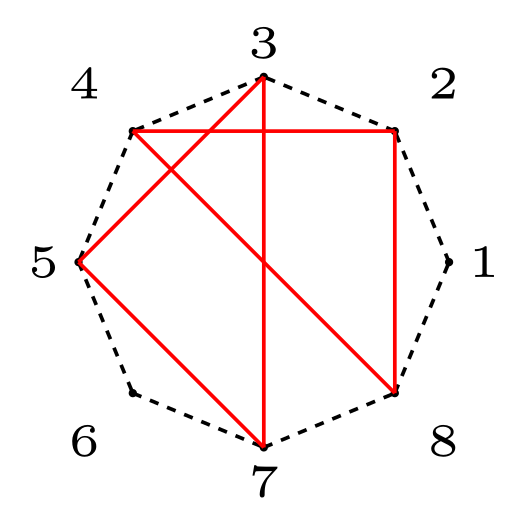
Trong trường hợp thứ ba, hai tam giác đã cho không bằng nhau.

Yêu cầu: hãy đưa ra số tam giác phân biệt trong tất cả các tam giác có thể tạo từ \(n\) đỉnh của đa giác.

Input

• Dòng đầu tiên chứa duy nhất một số nguyên dương \(n\).

Output

• Chứa một số nguyên duy nhất là số tam giác phân biệt.

Scoring

• Subtask 1 (\(10\%\) số điểm): \(n \leq 100\).
• Subtask 2 (\(20\%\) số điểm): \(n \leq 1000\).
• Subtask 3 (\(30\%\) số điểm): \(n \leq {10}^5\).
• Subtask 4 (\(40\%\) số điểm): \(n \leq {10}^9\).

3

1

10

8

20

33

Cho một đơn đồ thị vô hướng \(n\) đỉnh \((2 \leq n \leq {10}^5)\), \(m\) cạnh, đồ thị không có khuyên và cạnh song song. Ta có thể thực hiện phép "hợp" hai đỉnh \(u\) và \(v\) (không có cạnh nối trực tiếp) lại như sau:

• Thêm một đỉnh \(x\) vào đồ thị.
• Nối các cạnh \((x, w)\) trong đó \(w\) là đỉnh có cạnh nối tới u hoặc v.
• Xóa đỉnh \(u\) và \(v\) ra khỏi đồ thị.

Yêu cầu: Hãy thực hiện một số thao tác "hợp" như trên để biến đồ thị ban đầu thành một "đường thẳng". Nếu có nhiều cách thực hiện thì hãy đưa ra một cách bất kì.

Một đồ thị được gọi là đồ thị "đường thẳng" khi và chỉ khi thỏa mãn hai điều kiện sau

• đồ thị liên thông,
• có đúng hai đỉnh có bậc là \(1\), và \(n-2\) đỉnh còn lại có bậc là \(2\).

Đồ thị "đường thẳng" có dạng như sau:

Input

• Dòng đầu tiên gồm hai số nguyên dương \(n, m ~ \left(1 \leq m \leq \min\left({10^5}, \frac{n(n-1)}{2} \right) \right)\).
• \(m\) dòng tiếp theo, dòng thứ \(i ~ (1 \leq i \leq m)\) chứa hai số nguyên dương \(u_i, v_i ~ (1 \leq u_i, v_i \leq n, u_i \neq v_i)\) biểu diễn một cạnh nối của đồ thị, tức là cạnh thứ \(i\) nối hai đỉnh \(u_i\) và \(v_i\).

Output

Nếu không thể làm đồ thị đã cho trở thành một "đường thẳng" thì đưa ra duy nhất một số nguyên \(-1\).

Nếu có thể thì hãy đưa ra đáp án của bạn theo định dạng sau:

• Dòng đầu tiên chứa một số nguyên không âm \(q ~ (0 \leq q \leq n - 1)\) là số phép "hợp" bạn sử dụng.
• \(q\) dòng tiếp theo, mỗi dòng gồm hai số nguyên \(u_i, v_i ~ (1 \leq u_i, v_i < n + i)\) thể hiện rằng tại lần sử dụng phép "hợp" thứ \(i ~ (1 \leq i \leq q)\), hai đỉnh \(u_i\) và \(v_i\) được hợp lại thành đỉnh \(x_i = n + i\).

Scoring

• Subtask 1 (\(10\%\) số điểm): \(n \leq 10\).
• Subtask 2 (\(30\%\) số điểm): \(n \leq 20\).
• Subtask 3 (\(30\%\) số điểm): \(n \leq 3000\).
• Subtask 4 (\(30\%\) số điểm): \(n \leq {10}^5\).

2 1
1 2

0

4 4
1 2
2 3
3 4
4 1

1
1 3

3 3
1 2
2 3
1 3

-1

Cho \(q ~ (q \leq {10}^5)\) truy vấn, mỗi truy vấn cho hai số nguyên dương \(x, y\). Tìm số thao tác ít nhất để biến đổi \(x\) thành \(y\), biết rằng mỗi thao tác được thực hiện một trong hai hành động sau:

• Phép nhân 2 : \(x \gets x \times 2\).
• Phép trừ 1 (chỉ thực hiện được khi \(x > 1\)) : \(x \gets x - 1\).

Input

• Dòng đầu tiên gồm một số nguyên dương \(q\) là số truy vấn.
• \(q\) dòng tiếp theo, dòng thứ \(i ~ (1 \leq i \leq q)\) gồm hai số nguyên dương \(x_i, y_i ~ (x_i, y_i \leq {10}^9)\) thể hiện một truy vấn tìm số thao tác ít nhất để biến đổi từ \(x_i\) thành \(y_i\).

Output

• Gồm \(q\) dòng, mỗi dòng gồm một số nguyên duy nhất là kết quả của một truy vấn. Các kết quả phải được in theo thứ tự với các truy vấn trong dữ liệu đầu vào.

Scoring

• Subtask 1 (\(20\%\) số điểm): \(q \leq 1000\) và \(1 \leq x_i, y_i \leq 1000\).
• Subtask 2 (\(20\%\) số điểm): Tồn tại một cách tối ưu để biến đổi mà chỉ sử dụng phép nhân 2 nhiều nhất một lần.
• Subtask 3 (\(30\%\) số điểm): Tồn tại một cách tối ưu để biến đổi mà chỉ sử dụng phép trừ 1 nhiều nhất một lần.
• Subtask 4 (\(30\%\) số điểm): Không có ràng buộc gì thêm.

3
1 4
2 5
6 5

2
4
1