LQDOJ Contest #7 - OI Contest - Ngày 1

_minhduc - không gia đình, không người thân, không bạn bè. Đó là một quá khứ u buồn của cậu ấy. Do hoàn cảnh đặc biệt đó nên đã sinh ra một con người với tính cách khá giống các nhân vật "phản diện" trong các bộ phim hoạt hình. Tình cờ một ngày gặp được shiba, một con người cũng giống như _minhduc nhưng lại có một cô bạn gái rất xinh đẹp. Trùng hợp là shiba lại đồng ý làm bạn với _minhduc, từ đó câu chuyện của chúng ta bắt đầu.

Như các bạn đã biết, _minhduc là một người nghiện máy tính, cụ thể là nghiện ba thứ: nghiện code, nghiện trò chơi điện tử, nghiện phim hoạt hình. Trong các trò chơi điện tử mà _minhduc từng chơi qua, cậu ấy tâm đắc nhất với hai trò chơi, đó là hai trò chơi A của nhà G và V của nhà R. Kĩ năng của cậu ấy có thể nói là thượng thừa ở cả hai trò chơi này.

Trùng hợp thay, shiba đang có ý định thành lập đội tuyển thể thao điện tử Esports và cần người thành thạo trong hai trò chơi này. Do kĩ năng thượng thừa của _minhduc, cậu ấy quen khá nhiều người chơi giỏi. Cậu ấy có \(n\) người bạn, những người bạn đó đều chơi cả hai trò chơi trên, khi được _minhduc mời để giới thiệu vào đội tuyển, họ đều đồng ý.

Có thể biểu diễn mức độ kĩ năng của một người chơi dưới dạng một số nguyên dương \(a\). Trong biểu diễn ở hệ nhị phân của số nguyên \(a\) này gồm \(20\) bit (nếu không đủ \(20\) bit thì ta thêm các bit \(0\) vào bên trái sao cho đủ \(20\) bit). Sau đó, số này được chia thành hai phần, một phần gồm \(10\) bit bên trái và một phần gồm \(10\) bit bên phải. Phần \(10\) bit bên trái được đưa về hệ thập phân và đó là mức độ kĩ năng ở tựa game A của người này, coi là \(x\). Phần \(10\) bit bên phải cũng được đưa về hệ thập phân và đó là mức độ kĩ năng ở tựa game V của người này, coi là \(y\). Mỗi người chơi đều có một số nguyên biểu diễn mức độ kĩ năng của người đó. Độ chênh lệch kĩ năng giữa hai người \(i\) và \(j\) bằng \(\max(|x_{i}-x{j}|,|y_{i}-y_{j}|)\). Độ chênh lệch kĩ năng của \(k\) người bất kì bằng giá trị lớn nhất của độ chênh lệch kĩ năng giữa hai người bất kì trong \(k\) người này.

shiba khi này cần chọn lấy \(k\) thành viên để tham gia giải vô địch Flower_On_Stone League. Tuy nhiên, để có thể giao tiếp tốt hơn, cậu ấy quyết định chọn các thành viên sao cho độ chênh lệch kĩ năng giữa \(k\) thành viên là nhỏ nhất có thể, như vậy họ mới hiểu ý nhau. _minhduc quyết định sẽ cài một chương trình để tính toán việc này, thế nhưng Macbook M2 Pro của cậu ấy đang bị hỏng và phải đem đi sửa chữa. Bạn hãy giúp cậu ấy nhé ~(để cậu ấy còn lấy được sự tin tưởng của shiba để còn thực hiện bước tiếp theo của kế hoạch chứ muahahahaha)~.

Yêu cầu: Đưa ra một số nguyên dương duy nhất là độ chênh lệch kĩ năng nhỏ nhất có thể.

Input

• Dòng thứ nhất chứa một số nguyên dương \(\phi\) - số thứ tự của subtask chứa test đó \((1 \le \phi \le 6)\).
• Dòng thứ hai chứa hai số nguyên dương \(n,k\) (\(1 \le n \le 10^5, 1 \le k \le n\)).
• Dòng thứ ba chứa \(n\) số nguyên dương \(a_{1},a_{2},...,a_{n}\) (\(1 \le a_i \le 2^{20}-1\)).

Output

• Gồm một dòng chứa một số nguyên duy nhất là kết quả bài toán.

Scoring

• Subtask \(1\) (\(10\%\) số điểm): \(n = k\).
• Subtask \(2\) (\(10\%\) số điểm): \(1 \le k \le n \le 20\).
• Subtask \(3\) (\(15\%\) số điểm): \(0 \le a_{i} \le 1023\).
• Subtask \(4\) (\(15\%\) số điểm): \(0 \le x_{i}, y_{i} \le 50\).
• Subtask \(5\) (\(20\%\) số điểm): \(0 \le x_{i}, y_{i} \le 200\).
• Subtask \(6\) (\(30\%\) số điểm): không có ràng buộc gì thêm.

Example

1
3 3
1 2 3

2

Sau khi giới thiệu tuyển thủ cho shiba, cậu ấy đã phần nào tin tưởng hơn _minhduc. Trùng hợp thay, lúc đó một biến cố đã xảy ra, đó là shiba bị bạn gái đá. Liệu chuyện gì sẽ xảy ra kế tiếp?

_minhduc là một đá thủ, chuyên sưu tầm các tảng đá. Hôm nay, bất ngờ tìm được một khu vực có "view triệu đô" - biển xanh, mây trắng, nắng vàng, _minhduc quyết định mang các tảng đá của mình tới để xây dựng thành một đoạn đường.

_minhduc có \(n\) tảng đá, tảng đá thứ \(i\) có trọng lượng là \(w_i\), khi nhảy lên trên chúng sẽ phát ra một loại âm thanh, để thuận tiện thì ta đánh số chúng trùng với trọng lượng của tảng đá, gọi là chất âm. Các tảng đá có thể khác nhau về trọng lượng cũng như chất âm, nhưng trọng bộ sưu tầm có rất nhiều đá của _minhduc vẫn có thể tồn tại hai hoặc nhiều tảng đá cùng trọng lượng và chất âm. _minhduc ban đầu xếp chúng thành một con đường thẳng, từ tảng đá thứ \(1\) cho tới tảng đá thứ \(n\). Khi nhảy từ tảng đá đầu tiên tới tảng đá cuối cùng, ta nhận được một "bản nhạc" khá vui tai. Sau đấy cậu ấy đã gọi điện cho bạn gái cũ của shiba để mời cô ấy đến thử đoạn đường này và ngắm nhìn khung cảnh tuyệt đẹp kia.

Tuy nhiên, ngay trước thời điểm cô ấy đến, _minhduc bỗng muốn thay đổi "bản nhạc" kia. Cậu ấy có thể làm thao tác sau vô số lần, đó là chọn hai tảng đá liền kề có tổng trọng lượng không quá \(k\) và đổi chỗ chúng. Sau khi đổi chỗ, cậu ấy sẽ lại thử nhảy từ tảng đá thứ \(1\) tới tảng đá thứ \(n\) và lại thu được một "bản nhạc".

Cậu ấy tự hỏi, nếu cứ thực hiện các thao tác trên, sẽ thu được bao nhiêu "bản nhạc" khác nhau. Hai "bản nhạc" được coi là khác nhau nếu có ít nhất một vị trí mà chất âm của tảng đá giữa chúng khác nhau. ~Cậu ấy cần biết có bao nhiêu "bản nhạc" khác nhau để còn trổ tài "làm nhạc" cho cô bạn gái cũ của shiba biết chứ.~

Yêu cầu: Đếm số "bản nhạc" khác nhau có thể thu được.

Input

• Dòng đầu tiên chứa số nguyên dương \(\phi\) - số thứ tự của subtask chứa test đó \((1 \le \phi \le 6)\).

• Dòng tiếp theo chứa hai số nguyên dương lần lượt là \(N\) và \(K\) – lần lượt là số tảng đá và tổng trọng lượng tối đa của hai tảng đá liền kề _minhduc có thể chọn để hoán đổi \((1 \le N \le 3 \times 10^5, 1\le K \le 10^9)\).

• Dòng cuối cùng chứa \(N\) số nguyên dương \(w_1,w_2,...,w_N\) \((1 \le w_i \le 10^9)\).

Output

• In ra kết quả bài toán sau khi chia lấy dư cho \(10^9+7\).

Scoring

• Subtask \(1\) (\(10\%\) số điểm): Có \(N \le 7\).

• Subtask \(2\) (\(10\%\) số điểm): Có \(N \le 100\) và tất cả chất âm của các tảng đá đều khác nhau đôi một.

• Subtask \(3\) (\(15\%\) số điểm): Có \(N \le 1000\) và tất cả chất âm của các tảng đá đều khác nhau đôi một.

• Subtask \(4\) (\(20\%\) số điểm): Có \(N \le 1000\).

• Subtask \(5\) (\(25\%\) số điểm): Có \(N \le 10^5\) và tất cả chất âm của các tảng đá đều khác nhau đôi một.

• Subtask \(6\) (\(20\%\) số điểm): Không có ràng buộc gì thêm.

Example

1
4 8
3 5 3 7

3

Sau khi dẫn cô gái ấy đi trên đoạn đường "biết hát" kia, _minhduc đã nhận được cảm tình của cô ấy. Tuy nhiên, ở đây, shiba lại đang rất "lụy" người yêu cũ, vì vậy đã tới lúc để _minhduc chơi đùa một chút...

shiba có một vườn hoa nho nhỏ. Cậu ấy quyết định sẽ trồng hoa để tặng hoa cho cô "người yêu cũ" kia để tỏ lòng thành. Khu vườn gồm \(N\) bồn hoa, được đánh số từ \(1\) đến \(N\), trong đó một số bồn hoa được kết nối bằng ống nước. Các bồn hoa và các ống nước tạo thành một cây, trong đó các bồn hoa là các nút và các ống nước là các cạnh. Mỗi bồn hoa có một máy bơm được lắp đặt có thể bơm nước từ dưới đất lên trên. Nước này sẽ được tưới cho bồn hoa mà máy bơm đó đặt và nó sẽ chảy qua các ống nước đến một số bồn hoa khác mà có đường ống kết nối đến chúng.

Các máy bơm được đánh số từ \(1\) đến \(N\) (số máy bơm bằng với số bồn hoa trong khu vườn). Nếu máy bơm đặt trong một bồn hoa có số thứ tự \(x\) (\(1 \le x \le N)\) hoạt động trong \(p\) phút, nước sẽ đến tất cả các bồn hoa có khoảng cách không quá \(p-1\) cạnh từ \(x\) trong cây (khoảng cách giữa hai đỉnh \(u\) và \(v\) bất kì là số cạnh \(u\) cần đi qua để đến tới \(v\)).

Hệ thống máy bơm được thiết kế sao cho một máy bơm chạy trước, sau đó là máy bơm khác và cứ tiếp tục như vậy (hai máy bơm không bao giờ hoạt động đồng thời, và một máy bơm chỉ có thể chạy một lần). Một bồn hoa được coi là đã được tưới nước nếu có nước đã tưới cho nó, không quan tâm nước đó là từ máy bơm nào. Các máy bơm được thiết kế sao cho nếu một máy bơm có số thứ tự \(i\) chạy, nó chỉ được chạy tối đa \(t_i\) phút. Một lần chạy của máy bơm phải kéo dài một số phút nguyên.

Tất cả các máy bơm đều tiêu thụ điện như sau:

• Một lần chạy trong \(1\) phút tốn \(c_1\) VND, \(2\) phút chạy tốn \(c_2\) VND và cứ tiếp tục như vậy. Nếu máy bơm không chạy, nó sẽ không tiêu thụ điện.

shiba cần tính được số tiền tối thiểu cần chi trả cho điện năng sao cho một bộ máy bơm phù hợp chạy để tất cả các bồn hoa đều được tưới. Tuy nhiên, do mải trồng hoa và cũng do quá đau buồn, cậu ấy quyết định nhờ cậy tới "người anh em" _minhduc của mình. ~Do rủ lòng thương~ nên _minhduc quyết định giúp, thế nhưng chiếc Macbook M2 Pro của cậu ấy vẫn chưa được sửa xong. Bạn hãy giúp cậu ấy nhé.

Yêu cầu: Xác định số tiền tối thiểu sao cho một bộ máy bơm phù hợp chạy, để tất cả các bồn hoa đều có thể được tưới.

Input

• Dòng đầu tiên chứa số nguyên dương \(\phi\) - số thứ tự của subtask chứa test đó \((1 \le \phi \le 7)\).

• Dòng thứ hai chứa số nguyên dương \(N\) \((1 \le N \le 2000)\) - số bồn hoa, cũng là số máy bơm.

• Dòng thứ ba chứa \(N\) số nguyên \(c_1,c_2,...,c_N\) (\(0 \le c_i \le 10^6)\) - số tiền điện năng mà một máy bơm chạy trong \(1,2,...,N\) phút.

• Dòng thứ tư chứa \(N\) số nguyên \(t_1,t_2,...,t_N\) (\(0 \le t_i \le N)\) - thời gian chạy tối đa cho mỗi máy bơm. Trong trường hợp \(t_i = 0\) thì máy bơm thứ \(i\) không sử dụng được.

• \(N-1\) dòng cuối cùng mỗi dòng chứa hai số \(u,v\) mô tả ống nước (cạnh) nối bồn hoa có số \(u\) và \(v\). Bộ dữ liệu đảm bảo rằng các bồn hoa và các ống nước nối với nhau tạo thành cây.

• Dữ liệu vào luôn đảm bảo rằng \(c_1 \le c_2 \le ... \le c_N\).

Output

• In ra số tiền tối thiểu thỏa mãn yêu cầu đề bài, nếu không có cách chọn thỏa mãn thì in ra \(-1\).

Scoring

• Subtask \(1\) (\(10\%\) số điểm): Có \(N \le 8\).

• Subtask \(2\) (\(10\%\) số điểm): Có \(N \le 75\) và cây có dạng đường thẳng.

• Subtask \(3\) (\(10\%\) số điểm): Có \(N \le 500\) và cây có dạng đường thẳng.

• Subtask \(4\) (\(15\%\) số điểm): Có \(N \le 2000\) và cây có dạng đường thẳng.

• Subtask \(5\) (\(15\%\) số điểm): Có \(N \le 75\).

• Subtask \(6\) (\(15\%\) số điểm): Có \(N \le 500\).

• Subtask \(7\) (\(25\%\) số điểm): Không có ràng buộc gì thêm.

Example

 1
 8
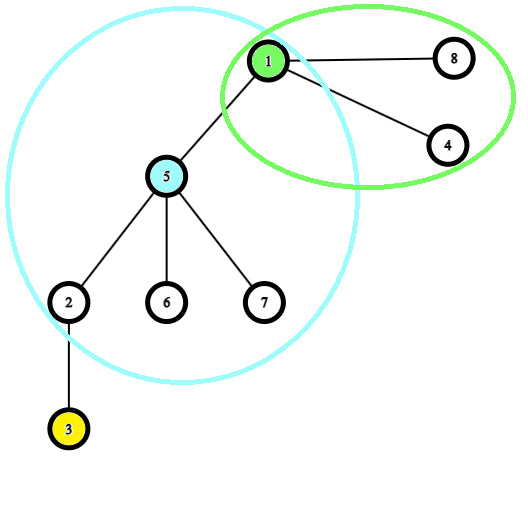
 1 2 5 7 8 14 20 29
 2 4 1 0 2 3 2 0
 2 5
 6 5
 5 7
 2 3
 1 8
 4 1
 1 5

5

2
8
1 2 4 8 10 12 24 26
1 4 3 8 2 5 6 0
8 7
5 4
2 3
2 1
7 6
5 6
4 3

6