5. LQDOJ Contest #6 - Bài 5 - CEO
Sau khi trở về từ chuyến đi chơi, vẫn bị cô ấy từ chối quay lại, đã thế lại còn yêu thằng khác giàu ngang thậm chí còn đẹp trai hơn ~cụ thể là yêu ~. Do quá cay cú, thề sẽ phải cố gắng thành lập công ti giàu nhất Việt Nam để trả thù cho cô "người yêu cũ" phải hối hận. Hai năm sau, đã trở thành CEO của một công ty lớn nhất Việt Nam như anh ấy đã thề, nhưng hiện nay công ty lại có một vấn đề "nho nhỏ"...
là CEO của một công ty với \(N\) nhân viên, đánh số từ \(1\) đến \(N\). Hệ thống tổ chức của công ty được phân theo các cấp bậc – mọi nhân viên, trừ nhân viên đánh số \(1\) thì mọi nhân viên đều có đúng một cấp trên trực tiếp. Nói cách khác, mọi nhân viên đều có \(1\) hoặc nhiều cấp dưới (trực tiếp hoặc gián tiếp) bao gồm cả chính nhân viên đó. Ví dụ, nhân viên đánh số \(1\) sẽ có chính xác \(N\) cấp dưới. Với mỗi nhân viên \(X\), ta gọi \(X\) là cấp dưới mức độ \(0\). Tiếp đó, các cấp dưới trực tiếp của nhân viên ấy sẽ gọi là cấp dưới mức độ \(1\). Và mọi cấp dưới trực tiếp của các nhân viên ấy (những nhân viên mà là cấp dưới trực tiếp của \(X\)) sẽ gọi là cấp dưới mức độ \(2\). Cách gọi này tương tự với các cấp dưới nữa.
Có một thông tin quan trọng mà một số nhân viên đã biết từ trước ~tin đó là cô người yêu cũ của sắp cưới với nhưng lại đang có bồ nhí ở ngoài~, và muốn cả công ty cùng biết đến. Nhiều lần, sẽ chọn ra nhân viên \(X\) và một giá trị nguyên \(K\), sau đó sẽ chia sẻ thông tin này cho các cấp dưới từ mức độ \(0\) đến mức độ \(K\) (nếu mức độ của cấp dưới của \(X\) cao nhất mà nhỏ hơn \(K\) thì ta chỉ xét đến đấy). Để cho đơn giản, ta sẽ gọi các cấp dưới này là “cấp dưới \(K\)”. Vấn đề của cách làm này là trong nhiều trường hợp, sẽ có nhiều nhân viên đã biết từ trước về thông tin cần chia sẻ, điều này có thể gây lãng phí thời gian và tài nguyên của công ty. Do đó muốn tính xem với các nhân viên \(X\) cần xét, số cấp dưới \(K\) của nhân viên \(X\) mà đã biết tin tức này là bao nhiêu.
Yêu cầu: Vì số lượng nhân viên quá lớn nên không thể tính một cách thủ công được. Anh ta muốn viết một chương trình để tính, nhưng làm CEO đã lâu nên không còn nhớ cách code. Bạn hãy giúp anh ấy lập chương trình để tính toán theo ý muốn của .
~tin chấn động như thế các bạn hãy giúp tính để anh ta còn rủ nhân viên của mình đi hóng drama bắt quả tang ngay trong đám cưới của cô người yêu cũ đi chứ :Đ~
Input
- Dòng đầu tiên chứa số nguyên \(N\) – số lượng nhân viên trong công ty của \((2 \le N \le 2 \times 10^5)\).
- \(N-1\) dòng tiếp theo, mỗi dòng chứa hai số nguyên \(x\) và \(y\) cho biết quan hệ giữa các nhân viên, cụ thể là nhân viên \(x\) sẽ là cấp trên trực tiếp của nhân viên \(y\)
- Dòng tiếp theo chứa \(N\) số nguyên nguyên: \(b_1, b_2, ..., b_N\) với hai giá trị là \(0\) hoặc \(1\), cho biết nhân viên thứ \(i\) có biết thông tin cần chia sẻ này từ trước hay không (ở đây \(1\) mang nghĩa là biết và \(0\) là không).
- Dòng tiếp theo chứa một số nguyên dương \(Q\) – số truy vấn \((1 \le Q \le 2 \times 10^5)\).
- \(Q\) dòng cuối cùng của bộ dữ liệu sẽ là các truy vấn của bài. Truy vấn gồm \(2\) loại gồm:
- Loại \(1\) (chia sẻ thông tin):
1 x k: thông báo thông tin tới tất cả cấp dưới \(K\) của nhân viên \(X\) \((0 \le K \le N)\). - Loại \(2\) (xác định số lượng):
2 x k: muốn xác định có bao nhiêu cấp dưới \(K\) của nhân viên \(X\) đã biết thông tin cần chia sẻ \((0 \le K \le N)\).
- Loại \(1\) (chia sẻ thông tin):
Output
- Với mỗi truy vấn loại \(2\), in ra một dòng là đáp án theo thứ tự của input.
Scoring
- Subtask \(1\) (\(10\%\) số điểm): Có \(N\le{10}^4,\ Q\le{10}^4\).
- Subtask \(2\) (\(20\%\) số điểm): Có \(k=N\) trong mọi truy vấn.
- Subtask \(3\) (\(20\%\) số điểm): Có tất cả các truy vấn là truy vấn loại \(2\).
- Subtask \(4\) (\(20\%\) số điểm): Có \(N\le{5\times10}^4,\ Q\le{5\times10}^4\).
- Subtask \(5\) (\(30\%\) số điểm): Không có ràng buộc gì thêm.
Example
Test 1
CEO.INP
10
1 2
1 3
3 4
3 5
3 6
4 7
4 8
8 9
8 10
0 1 0 1 0 1 0 1 0 1
9
2 1 1
2 4 4
2 3 0
1 1 2
2 3 4
1 4 1
2 1 1
2 4 4
2 3 2CEO.OUT
1
3
0
6
3
4
6Note
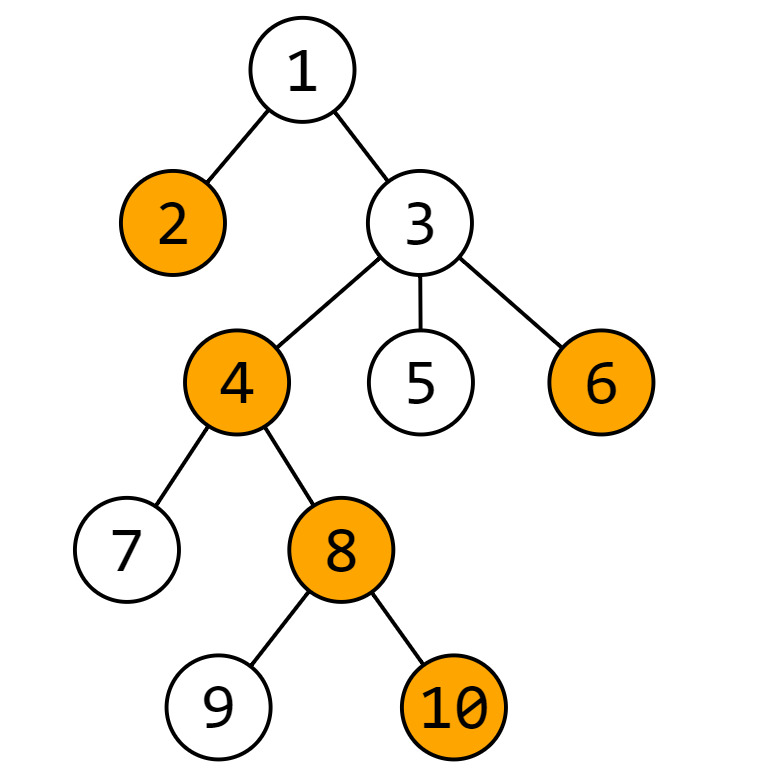
Biểu đồ trên cho biết mối quan hệ cấp trên – cấp dưới giữa các nhân viên trong công ty, màu cam cho biết nhân viên đó đã biết thông tin từ thời điểm ban đầu (lúc chưa chia sẻ thông tin lần nào).
- Với truy vấn đầu tiên
2 4 4:- Xét nhân viên số thứ tự \(4\), cấp dưới mức độ \(0\) là \(4\) (chính nó), mức độ \(1\) là nhân viên số \(7\) và \(8\) (cả hai đều là cấp dưới mức độ \(1\) của nhân viên số \(4\)), và mức độ \(2\) là nhân viên số \(9\) và \(10\). Nhìn vào hình vẽ ta dễ thấy rằng không tồn tại nhân viên cấp dưới nào của \(4\) có mức độ từ \(3\) trở đi.
- Nhân viên \(4, 8, 10\) đã biết thông tin từ trước, vậy nên câu trả lời cho truy vấn này là \(3\).
- Với truy vấn tiếp theo
1 4 1:- Cấp dưới \(1\) của nhân viên số \(4\) là \(4\), \(7\) và \(8\). Nhân viên số \(4\) và \(8\) đã biết thông tin từ trước, vậy nên chỉ có nhân viên số \(7\) là phải tiếp nhận thông tin này.
- Với truy vấn cuối cùng
2 4 4:- Cấp dưới \(4\) của nhân viên số \(4\) là \(4, 7, 8, 9\) và \(10\). Nhân viên số \(4\), \(7( * )\), \(8\) và \(10\) đã biết thông tin này, vậy nên đáp án cho truy vấn này là \(4\).
\(( * )\) Nhân viên số \(7\) ban đầu không biết nhưng về sau ở truy vấn thứ \(2\) thì đã được thông báo nên biết.
- Cấp dưới \(4\) của nhân viên số \(4\) là \(4, 7, 8, 9\) và \(10\). Nhân viên số \(4\), \(7( * )\), \(8\) và \(10\) đã biết thông tin này, vậy nên đáp án cho truy vấn này là \(4\).