OLP MT&TN 2023 Bảng Siêu Cúp

Bình là một nhà khảo cổ học đam mê khám phá bí ẩn về các triều đại cổ xưa. Lần này Bình phát hiện ra một bản đồ chứa thông tin về một căn hầm trong lòng đất có cất giữ bí ẩn về triều đại Chăm Pa ở khu vực Miền Trung - Tây Nguyên. Vốn là một nhà khảo cổ nhiều kinh nghiệm, để giảm thiểu tối đa rủi ro trong quá trình thám hiểm, Bình quan sát cẩn thận và giải mã những chi tiết trên bản đồ trước khi tiến vào khám phá căn hầm.

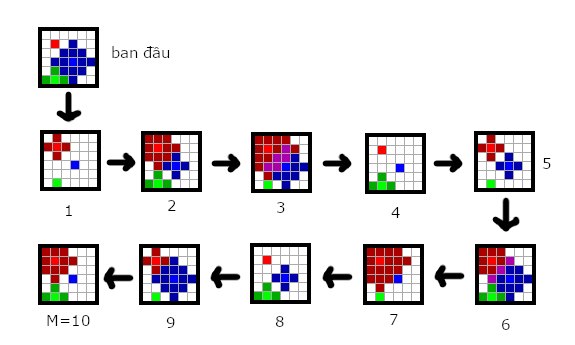
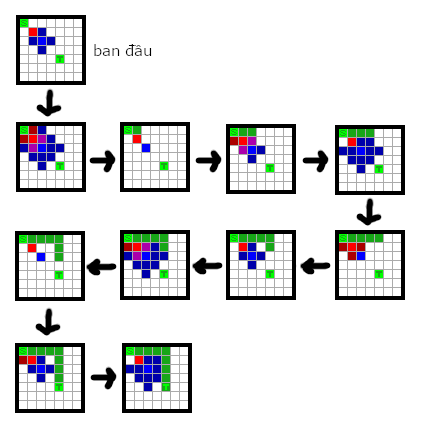
Bình phát hiện ra căn hầm được cho bởi một bảng kích thước \(N\times N\) ô vuông đơn vị. Các hàng và các cột của bảng được đánh số từ \(1\) đến \(N\). Trên bảng có \(K\) viên đá thạch anh, viên thứ \(i\) \((1\le i\le K\)) được đặt tại ô \((x_i,y_i)\), có hệ số phát sóng là \(r_i\) và phát sóng theo chu kỳ với \(r_i\) trạng thái, từ \(0\) đến \(r_i-1\), nếu một thời điểm viên đá ở trạng thái \(t\) thì thời điểm tiếp theo viên đá sẽ ở trạng thái \((t+1)\)%\(r_i\). Một viên đá ở trạng thái \(t\) sẽ phủ sóng chạm tới tất cả các ô nằm trong căn hầm có khoảng cách Manhattan nhỏ hơn hoặc bằng \(t\). Khoảng cách Manhattan giữa hai ô \((x_1,y_1)\) và ô \((x_2,y_2)\) bằng giá trị \(|x_1-x_2|+|y_1-y_2|\).

Sau một thời gian nghiên cứu, Bình tiếp tục phát hiện ra lối vào căn hầm sẽ xuống trực tiếp ô \((x_s,y_s)\) và ô lưu giữ bí ẩn về triều đại Chăm Pa là ô \((x_t,y_t)\). Bình cũng tính toán được thời điểm bước vào ô \((x_s,y_s)\) giá trị trạng thái của mỗi viên thạch anh trong căn hầm. Việc di chuyển trong căn hầm là theo từng ô, mỗi bước Bình chỉ có thể bước sang một trong bốn ô kề cạnh ngang hoặc dọc hoặc đứng yên tại ô đó. Mỗi bước tương ứng với một thời điểm chuyển trạng thái của các viên thạch anh. Nếu như Bình bước vào một ô trong tầm phủ sóng của một viên thạch anh nào đó thì cửa căn hầm sẽ tự động đóng lại và Bình sẽ gặp nguy hiểm.

Để chuẩn bị cho chuyến thám hiểm một cách an toàn nhất, Bình cần giải được hai câu hỏi sau:

1. Số lượng lớn nhất các ô bị phủ sóng tại một thời điểm bởi các viên thạch anh sau tối đa \(M\) bước là bao nhiêu?
2. Số lượng ít nhất bước để Bình di chuyển từ ô \((x_s,y_s)\) đến ô \((x_t,y_t)\) là bao nhiêu sao cho trong quá trình di chuyển Bình không đứng vào ô đang bị phủ sóng nào?

Yêu cầu: Biết được trạng thái của từng viên thạch anh, viên thứ \(i\) \((1\le i\le K)\) là trạng thái \(t_i\), tại thời điểm Bình vào hầm tại ô \((x_s,y_s)\), hãy giúp Bình trả lời hai câu hỏi trên.

Input

• Dòng đầu ghi bốn số nguyên dương \(Q\), \(N\), \(K\) và \(M\).
• Dòng thứ \(i\) trong số \(K\) dòng tiếp theo chứa \(4\) số nguyên dương \(x_i, y_i, r_i\) và \(t_i\).
• Dòng tiếp theo chứa hai số nguyên dương \(x_s\) và \(y_s\).
• Dòng cuối cùng chứa hai số nguyên dương \(x_t\) và \(y_t\).

Các số trên cùng một dòng cách nhau bởi dấu cách.

Output

• Nếu \(Q=1\), ghi ra một số nguyên duy nhất là số lượng lớn nhất các ô bị phủ sóng tại một thời điểm bởi các viên thạch anh sau tối đa \(M\) bước.
• Nếu \(Q=2\), ghi ra một số nguyên duy nhất là số lượng ít nhất bước để Bình di chuyển từ ô \((x_s,y_s)\) đến ô \((x_t,y_t)\) mà không gặp nguy hiểm. Ghi ra \(-1\) nếu như không tồn tại phương án di chuyển từ ô \((x_s,y_s)\) đến ô \((x_t,y_t)\) mà Bình không gặp nguy hiểm.

Constraints

• Tại mỗi bước di chuyển, Bình không bước ra khỏi phạm vi căn hầm \(N \times N\) ô.
• Dữ liệu đảm bảo tại thời điểm bước vào căn hầm, Bình không gặp nguy hiểm, nghĩa là ô \((x_s,y_s)\) không bị phủ sóng bởi bất kỳ một viên thạch anh nào.
• Có thể có trường hợp nhiều viên thạch anh được đặt cùng một ô.
• \(Q\in \{1,2\}\).
• \(3 \le N \le 500\).
• \(1 \le K \le 15000\).
• \(1\le M \le 1000\).
• \(0 \le t_i < r_i \le 6\), \(\forall i: 1 \le i \le K\).
• \(1 \le x_s, y_s, x_f, y_f \le N\).
• \(1 \le x_i, y_i \le N\), \(\forall i: 1 \le i \le K\).

Scoring

• Subtask 1 (\(27\) điểm): \(Q=1\) và \(M=10\).
• Subtask 2 (\(23\) điểm): \(Q=1\).
• Subtask 3 (\(17\) điểm): \(Q=2\) và \(r_i=1\), \(\forall i: 1\le i\le K\).
• Subtask 4 (\(13\) điểm): \(Q=2\); \(N\le 7\) và \(r_i\le 3\), \(\forall i: 1\le i\le K\).
• Subtask 5 (\(11\) điểm): \(Q=2\); \(t_i=0\), \(\forall i: 1\le i\le K\).
• Subtask 6 (\(9\) điểm): \(Q=2\).

Examples

1 6 3 10
2 2 4 0
6 2 2 1
4 4 3 2
1 1 
6 6

26

2 7 2 3 
2 2 2 0
3 3 3 1
1 1
5 5

10

Trong truyền thuyết thời xa xưa, Miền Trung - Tây Nguyên là một vùng đất rộng lớn với nguồn tài nguyên phong phú và ẩm thực đa dạng, đứng đầu bởi một vị vua anh minh. Tương truyền, các đơn vị số đo về khoảng cách, vận tốc, thời gian vào thời đó rất khác biệt, không cùng đơn vị đo lường như bây giờ.

Vùng đất này được tổ chức thành \(N\) thành phố và \(N-1\) cung đường hai chiều. Cung đường thứ \(i\) có độ dài \(w_i\) nối hai thành phố \(a_i\) và \(b_i\) với nhau, và các cung đường này được xây dựng để bảo đảm hai thành phố bất kỳ có thể đến được với nhau thông qua một hoặc nhiều cung đường khác nhau.

Là người ưa thích tìm tòi văn hoá các địa phương trong vương quốc của mình, đức vua đã triệu tập \(M\) cận vệ để đi khám phá. Người cận vệ thứ \(j\) \((1\le j\le M)\) được cấp một con chiến mã có thể chạy với vận tốc tối đa \(s_j\) (thời gian tăng tốc ban đầu không đáng kể). Anh ta sẽ xuất hành vào thời điểm \(t_j\) để đi từ thành phố \(u_j\) đến thành phố \(v_j\). Lưu ý rằng, thời điểm đặt chân lên một thành phố có thể là một số thực.

Yêu cầu: Cho biết \(Q\) thành phố, với mỗi thành phố, hãy cho biết thời điểm đầu tiên có một cận vệ của nhà vua đặt chân đến là khi nào.

Input

• Dòng đầu ghi ba số nguyên \(N, M\) và \(Q\) là số lượng thành phố, số người cận vệ và số thành phố được truy vấn.
• Dòng thứ \(i\) trong số \(N - 1\) dòng tiếp theo chứa \(3\) số nguyên \(a_i, b_i, w_i\) cho biết cung đường thứ \(i\) nối giữa hai thành phố \(a_i, b_i\) với độ dài \(w_i\).
• Dòng thứ \(j\) trong số \(M\) dòng tiếp theo chứa \(4\) số nguyên \(u_{j}, v_{j}, t_{j}, s_{j}\) cho biết tại thời điểm \(t_j\) người cận vệ thứ \(j\) sẽ lấy cỗ xe có tốc độ \(s_j\) để đi từ thành phố \(u_j\) đến \(v_j\).
• Dòng cuối cùng chứa \(Q\) số nguyên phân biệt \(k_1, k_2, \ldots, k_Q\) là số đỉnh mà đức vua quan tâm.

Output

• Ghi ra \(Q\) dòng, dòng thứ \(i\) chứa một số thực là thời điểm đầu tiên có một người cận vệ đặt chân tới thành phố \(k_Q\). Ghi ra \(-1\) nêu thành phố đó không có cận vệ nào đặt chân tới.

Đáp án của bạn được cho là đúng nếu sai số tuyệt đối so với đáp án của giám khảo không quá \(10^{-6}\).

Example

Test 1

Input

10 2 4
1 2 2
3 1 3
1 4 1
6 2 7
5 2 4
7 3 5
3 8 6
8 9 3
8 10 1
6 8 2 2
7 10 3 3
1 3 5 7

Output

6.5
4.66666666220797
-1
3

Note

Dưới đây là hình ảnh của vùng đất:\

Người cận vệ thứ \(1\) đến các thành phố \([6, 2, 1, 3, 8]\) lần lượt vào các thời điểm \([2, 5\dfrac{1}{2}, 6\dfrac{1}{2}, 8, 11]\).
Người cận vệ thứ \(2\) đến các thành phố \([7, 3, 8, 10]\) lần lượt vào các thời điểm \([3, 4\dfrac{2}{3}, 6\dfrac{2}{3}, 7]\).
Các thành phố 4, 5, 9 không được ghé thăm.

Tổng kết lại, đáp án của 10 thành phố trên theo thứ tự từ 1 đến 10 là: \([6\dfrac{1}{2}, 5\dfrac{1}{2}, 4\dfrac{2}{3}, -1, -1, 2, 3, 6\dfrac{2}{3}, -1, 7]\).
Đề bài yêu cầu đáp án của 4 thành phố \(1, 3, 5, 7\) nên chúng ta in ra 4 số: \(6\dfrac{1}{2}, 4\dfrac{2}{3}, -1, 3\).
Ở dòng thứ hai của đáp án mẫu, dù đáp án không hoàn toàn đúng, nhưng số \(4.66666666220797\) có sai số tuyệt đối nằm trong mức chấp nhận được.

Constraints

• \(1 \leq N \leq 2 \times 10^{5}\)
• \(1 \leq M \leq 2 \times 10^{5}\)
• \(1 \leq Q \leq 2 \times 10^{5}\)
• \(1 \leq a_{i}, b_{i} \leq N\) \(\forall 1 \leq i \leq N\)
• \(1 \leq w_{i} \leq 10^{9}\)
• \(1 \leq u_{i}, v_{i} \leq N\), \(\forall 1 \leq i \leq M\)
• \(1 \leq t_{i}, s_{i} \leq 10^{9}\), \(\forall 1 \leq i \leq M\)
• \(1 \leq k_{i} \leq N, k_{i} \neq k_{j}\), \(\forall 1 \leq i, j \leq Q, i \neq j\)

Scoring

• Subtask \(1\) (\(20\) điểm): \(1 \leq N, M \leq 5 \times 10^{3}\).
• Subtask \(2\) (\(18\) điểm): \(a_{i} = \left \lfloor \dfrac{i + 1}{2} \right \rfloor, b_{i} = i + 1, 1 \leq i \leq N - 1\).
• Subtask \(3\) (\(16\) điểm): \(Q \le 10\).
• Subtask \(4\) (\(14\) điểm): \(s_1 = s_2 = \ldots = s_M\), \(v_{i} = 1\) \(\forall 1 \leq i \leq M\).
• Subtask \(5\) (\(12\) điểm): \(s_1 = s_2 = \ldots = s_M\).
• Subtask \(6\) (\(11\) điểm): Mỗi thành phố được kết nối trực tiếp với không quá hai con đường.
• Subtask \(7\) (\(9\) điểm): Không có ràng buộc gì thêm.

Miền Trung - Tây Nguyên ngày nay là một vùng đất tiềm năng giàu khoáng sản chưa được khai thác nhiều. Một dự án khai thác mỏ sắt nơi đây dự định xây dựng \(N\) địa điểm và \(M\) con đường nối giữa các cặp điểm, các địa điểm được đánh số từ \(1\) đến \(N\), các con đường được đánh số từ \(1\) đến \(M\). Con đường thứ \(i\) có chi phí xây dựng \(C_i\), giá trị sử dụng \(V_i\) và nối địa điểm \(x_i\) với \(y_i\) cho phép đi lại theo cả hai chiều. Có thể có nhiều con đường nối cùng một cặp điểm. Có \(Q\) địa điểm đặc biệt nơi mà khoáng sắt tập trung nhiều là \(k_1, k_2, \ldots, k_Q\).

Ban quản lý dự án muốn chọn ra một số con đường để xây dựng, sao cho tổng giá trị sử dụng lớn hơn hoặc bằng \(V^ *\), bảo đảm đi lại giữa \(Q\) địa điểm đặc biệt, và tổng chi phí xây dựng là càng nhỏ càng tốt. Hãy giúp họ tìm ra một phương án.

Đây là bài toán chỉ cần nộp các file kết quả đầu ra (OUTPUT-ONLY). Thí sinh được cho 20 file đầu vào tương ứng với 20 test, đối với mỗi file đầu vào thí sinh cần nộp một file kết quả đầu ra tìm được. Với mỗi file kết quả đầu ra đúng đắn, điểm của thí sinh được tính theo công thức trong phần Scoring.

Input

Thí sinh tải đầu vào tại đường dẫn: https://lqdoj.edu.vn/media/uploads/olp4ck3c.zip
Sau khi giải nén, bạn có 20 file đầu vào được đặt tên là 01.inp, 02.inp, ..., 20.inp, mỗi file mô tả một test theo định dạng:

• Dòng đầu ghi bốn số nguyên \(N\), \(M\), \(Q\) và \(V^ *\) (\(1 \leq N,M,Q \leq 1000\), \(1 \leq V^* \leq 10^9\));
• Dòng thứ \(i\) trong số \(M\) dòng tiếp theo chứa bốn số nguyên \(x_i, y_i, C_i, V_i\) (\(1 \leq x_i, y_i \leq n\), \(1 \leq c_i, v_i \leq 10^6\));
• Dòng tiếp theo chứa \(k_1, k_2, \ldots, k_Q\) (\(1 \leq k_i \leq n\)).

Dữ liệu bảo đảm \(V^ *\) không vượt quá tổng giá trị sử dụng của tất cả các cạnh, và nếu xây dựng cả \(M\) cạnh thì luôn đảm bảo đi lại giữa \(Q\) đỉnh đặc biệt.

Output

Với file đầu vào name.inp, bạn cần xuất ra file đầu ra name.out chứa kết quả test tương ứng theo định dạng:

• Dòng đầu ghi một số nguyên là tổng chi phí xây dựng tìm được;
• Dòng thứ hai ghi một số nguyên \(T\) là số cạnh được xây dựng, theo sau bởi \(T\) số nguyên dương là chỉ số của các cạnh đó.

Mỗi lần nộp bài bạn có thể nộp một hoặc nhiều file đầu ra, bạn cần nén các file đầu ra này lại thành submission.zip để nộp. Ở mục chọn ngôn ngữ của trang nộp bài, chọn "Output".

Subtasks

• Subtask 1 (\(5\) điểm): \(M \leq 20\);
• Subtask 2 (\(5\) điểm): \(V^*=1, Q=N\);
• Subtask 3 (\(10\) điểm): \(V^ * =1\);
• Subtask 4 (\(15\) điểm): \(Q=N\);
• Subtask 5 (\(65\) điểm): Không có ràng buộc gì thêm.

Examples

6 6 2 6
1 5 2 2
1 3 5 5
2 5 2 1
2 3 2 3
3 5 2 1
4 6 1 4
1 3

5
3 1 5 6

Scoring

Đối với mỗi test, bạn sẽ bị \(0\) điểm nếu đầu ra không hợp lệ; ngược lại, gọi \(C\) là tổng chi phí xây dựng các cạnh mà bạn tìm được, Ban tổ chức có một giá trị \(J\) đối với test đó:

• Nếu \(\frac{C}{J} < 1\) bạn được 1 điểm cho test đó;
• Nếu \(1 \leq \frac{C}{J} \leq 2\) bạn được \((\frac{2J-C}{J})^3 \times 100\%\) số điểm cho test đó;
• Nếu \(\frac{C}{J} > 2\) bạn được 0 điểm cho test đó.
• Trong quá trình thi, nếu bài làm của bạn tốt hơn của ban tổ chức ở một test nào đó, kết quả này sẽ được cập nhật cho ban tổ chức và dùng để chấm điểm cho các thí sinh khác. Việc cập nhật sẽ được thực hiện nhiều lần trong suốt quá trình thi mà không có thông báo gì thêm.

Điểm của lần nộp là tổng điểm đạt được của các test. Điểm của bài là điểm lớn nhất trong số các lần nộp.