Giao lưu Tin học trẻ Mở rộng Bảng C1 - Lần 1 - 2023

Vì quá mệt khi phải tìm ý tưởng để viết cốt truyện cho đề ôn Tin học trẻ lần này, Quý quyết định chọn 1 bài tập ngẫu nhiên để làm giải trí. Bài tập mà Quý chọn có đề bài như sau:

Cho \(1\) dãy \(A\) gồm \(n\) số nguyên dương và \(1\) số \(e\). Hãy đếm số cặp \((i,k)\) thỏa mãn các điều kiện sau:

• \(1 \le i, k\)
• \(i + e \times k \le n\)
• Tích \(a_i \times a_{i + e} \times a_{i + 2e} \times ... \times a_{i + ke}\) là 1 số nguyên tố

Nhắc lại, số nguyên tố là số lớn hơn \(1\) và chỉ có \(2\) ước dương là \(1\) và chính nó.

Tuy nhiên, Quý đã không còn đủ sức để làm được bài này nên muốn nhờ các bạn hãy thay Quý giải bài tập trên.

Input

• Dòng đầu tiên gồm số nguyên \(t\) (\(t \le 10\)) là số lượng test cases của bài toán.

Mỗi test có cấu trúc như sau:

• Dòng đầu tiên bao gồm \(2\) số nguyên dương \(n\) và \(e\) (\(1 \le e \le n \le 10^5\)) là kích thước của mảng \(A\) và số \(e\) đề bài cho.
• Dòng thứ \(2\) bao gồm \(n\) số nguyên dương \(a_1, a_2, a_3, ..., a_n\) \((a_i \le 10^6)\)

Output

• Với mỗi test, in ra \(1\) số nguyên là số lượng cặp (\(i\), \(k\)) thỏa mãn điều kiện đề bài trên một dòng.
• In ra tổng cộng \(t\) dòng cho \(t\) test.

Scoring

• Subtask \(1\) (\(30\%\) số điểm): \(n, e \le 200, a_i \le 10^3\)
• Subtask \(2\) (\(30\%\) số điểm): \(e = 1, n \le 10^5, a_i \le 10^3\)
• Subtask \(3\) (\(40\%\) số điểm): Không có ràng buộc gì thêm

6
7 3
10 2 1 3 1 19 3
3 2
1 13 1
9 3
2 4 2 1 1 1 1 4 2
3 1
1 1 1
4 1
1 2 1 1
2 2
1 2

2
0
4
0
5
0

(Ở một tương lai xa xôi) Trên con đường mới được quy hoạch của thành phố X, có \(n\) tòa nhà cao tầng nằm trên một con đường (tạm coi như một đường thẳng). Nhà thứ \(i\) có độ cao là \(h_i\) mét.
Việt không thích những tòa nhà có cùng độ cao nằm gần nhau. Cậu định nghĩa một dãy nhà \([l,r] (l\le r)\) là "nhàm chán" nếu như trong toàn bộ những căn nhà thứ \(l,l+1,l+2,\dots,r-1,r\) chỉ có không quá \(k\) độ cao khác nhau.
Nhằm đánh giá con đường này, Việt cần tính số lượng dãy nhà nhàm chán. Vì đã thấm mệt sau khi đi từ đầu đường tới cuối đường để lấy thông tin về chiều cao của các tòa nhà, Việt nhờ bạn lập trình giải quyết vấn đề trên. Hãy giúp Việt nhé!
Bonus: sau khi hỏi thị trưởng, Việt đã có được một số thông tin giúp việc tính toán trở nên dễ dàng hơn. Thông tin này được kí hiệu bởi số \(\theta\)

Input

• Dòng đầu tiên chứa \(\theta\) \((\theta \in \{1,2,3,4,5\})\): thông tin mới có được từ thị trưởng
• Dòng thứ hai chứa \(n,k\) \((1 \le n,k \le 10^5)\): số tòa nhà, và số định nghĩa sự "nhàm chán"
• Dòng tiếp theo chứa \(n\) số nguyên dương \(h_1, h_2, h_3, \dots, h_n (1 \le h_i \le 10^9)\)

Output

• Dòng duy nhất chứa số dãy nhà nhàm chán mà bạn đếm được

Scoring

• Subtask 1 (\(20\%\) số điểm): \(\theta = 1, h_i \le n \le 100\)
• Subtask 2 (\(30\%\) số điểm): \(\theta = 2, h_i \le n \le 1000\)
• Subtask 3 (\(15\%\) số điểm): \(\theta = 3\) và các tòa nhà có chiều cao khác nhau đôi một.
• Subtask 4 (\(15\%\) số điểm): \(\theta = 4, k = 1\)
• Subtask 5 (\(20\%\) số điểm): \(\theta = 5\), không có ràng buộc gì thêm.

1
5 2
1 2 3 1 1

10

Cho dãy số \(a\) gồm \(n\) số nguyên không âm. Bạn được thực hiện thao tác: đổi chỗ hai vị trí liên tiếp trong mảng \(a\) không quá \(k\) lần. Hãy tìm cách đổi để thu được dãy có thứ tự từ điển lớn nhất.

Input

• Dòng đầu tiên chứa hai số \(n,k\): độ dài dãy và số thao tác cho phép \((1 \le n \le 10^5, 0 \le k \le 5.10^9)\).
• Dòng tiếp theo chứa \(n\) số nguyên không âm \(a_1, a_2, a_3, \dots, a_n (0 \le a_i \le 10^9)\)

Output

• Dòng duy nhất chứa dãy \(a\) sau biến đổi mà có thứ tự từ điển lớn nhất.

Scoring

• Subtask 1 (\(25\%\) số điểm): \(n \le 5000\)
• Subtask 2 (\(75\%\) số điểm): \(n \le 10^5\)

4 2
1 3 2 4

3 2 1 4 

Thành phố Đà Nẵng vừa mới mở một khu du lịch ăn uống Danang Éating Park (DÉP). Tên thì giống công viên phần mềm, mà nhìn trông cũng na ná Chợ đêm Sơn Trà.

Theo quy hoạch, khu du lịch sẽ mở ra \(n\) kiosk ăn uống, khu thứ \(i\) có khả năng hút khách tự thân là \(w_i\). Các kiosk sẽ được nối với nhau bằng \(m\) con đường hai chiều, mỗi con đường kết nối hai kiosk khác nhau. Để đảm bảo trật tự, Ban quản lý DÉP đã thiết kế, xây dựng sao cho: không có hai con đường nào cùng nối hai thành phố lại với nhau, và từ một thành phố luôn có thể đi tới các thành phố khác thông qua \(m\) con đường đã xây. Nói cách khác, đây chính là đồ thị đơn vô hướng liên thông, có trọng số ở đỉnh.

GSPVH sau khi chơi đủ 3 triệu để nâng hạng thẻ Helio từ Hồng lên Vàng, thì rất được Helio quan tâm. Biết rằng Giáo sư rất thích trà sữa, Helio hỏi ông có muốn mở một cửa hàng trà sữa trong khuôn viên của DÉP hay không, nếu có thì họ sẽ hỗ trợ Giáo sư cả về chi phí lẫn thủ tục (đúng là thẻ vàng có khác)

Đúng lúc này, sau khi xem xét luồng giao thông đường (đi) bộ dự kiến, Ban quản lý quyết định sẽ định chiều toàn bộ \(m\) con đường này lại, biến chúng thành đường một chiều hết, đồng thời xây dựng vài cọn đường nhỏ để nếu có ai bí đường không thể quay lại thì có thể men theo chúng, nhưng chúng ta không cần quan tâm tới những con đường này.

Vì sự thay đổi này, nên sau khi định chiều đồ thị, khả năng hút khách thực sự \(p_u\) của khu thứ \(u\) sẽ bằng tổng khả năng hút khách tự thân \(w_v\) của các đỉnh \(v\) có thể đi được từ \(u\).

Để đảm bảo sự công bằng cũng như thu hút nhiều khách du lịch nhất có thể, Ban quản lý Danang Éating Park mong muốn định chiều \(m\) cạnh sao cho \(p_u\) nhỏ nhất trong số \(n\) khu bán hàng là lớn nhất có thể. Biết rằng GSPVH có nhiều đàn em như bạn, ban quản lý nhờ Giáo sư hỏi bạn xử lý bài toán này. Hãy giúp họ nhé!

Input

• Dòng đầu tiên chứa hai số \(n, m\) \((1 \leq n, m \leq 4 \times 10^{5})\) - là số kiosk và số đường đi trong khu ăn uống DÉP.
• Dòng thứ hai chứa \(n\) số nguyên \(w_1, w_2, \ldots, w_n\) \((1 \leq w_i \leq 10^{9})\) - \(w_i\) là khả năng hút khách tự thân của đỉnh \(i\)
• \(m\) dòng tiếp theo, mỗi dòng chứa hai số \(u\), \(v\) \((1 \leq u, v \leq n)\) thể hiện một đường đi giữa hai kiosk \(u\) và \(v\).

Output

• Dòng đầu tiên in ra một số nguyên thể hiện khả năng hút khách nhỏ nhất trong phương án tối ưu.
• \(m\) dòng tiếp theo, mỗi dòng chứa hai số nguyên \(u\) và \(v\) thể hiện con đường được định chiều từ \(u\) đến \(v\).

Scoring

• Subtask \(1\) (\(20\%\) số điểm): \(n, m \le 20\).
• Subtask \(2\) (\(20\%\) số điểm): \(n, m \le 2000\).
• Subtask \(3\) (\(20\%\) số điểm): \(m < n\).
• Subtask \(4\) (\(20\%\) số điểm): \(w[i] = w[i + 1] \forall 1 \leq i \leq n - 1\).
• Subtask \(5\) (\(20\%\) số điểm): Không có giới hạn gì thêm.

Sample

Test 1

Input

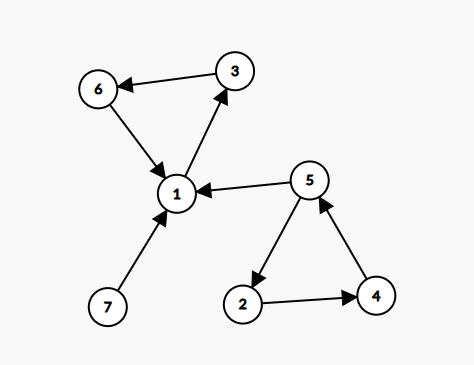
7 8
1 2 2 3 1 3 4
2 4
2 5
6 3
1 3
1 7
4 5
1 6
5 1

Output

6
2 4
5 2
3 6
1 3
7 1
4 5
6 1
5 1
****
*********

Note

Đây là biểu diễn đồ thị của đáp án được đưa ra:

Khi đó, \(p = {6, 12, 6, 12, 12, 6, 10}\), vì vậy \(\min p_i = p[1] = 6\).
Có thể chứng minh được không có cách định chiều đồ thị nào có \(\min p_i < 6\).