Tin học trẻ C - Bắc Ninh - Quảng Bình - Hưng Yên 2024

Cho dãy \(a\) gồm \(n\) số nguyên.

Bạn phải trả lời \(q\) truy vấn, mỗi truy vấn cho hai số nguyên \(b,c\), bạn cần tìm số cặp \((i,j)\) thoả mãn:

• \(1 \le i < j \le n\).
• \(a_i + a_j = b\).
• \(a_i \times a_j = c\).

Input

• Dòng thứ nhất chứa một số nguyên dương \(n\) (\(1 \le n \le 2 \times 10^5\)).
• Dòng thứ hai chứa \(n\) số nguyên \(a_1,a_2,...,a_n\) (\(1 \le |a_i| \le 10^9\)).
• Dòng thứ ba chứa một số nguyên dương \(q\) (\(1 \le q \le 2 \times 10^5\)).
• \(q\) dòng tiếp theo, mỗi dòng chứa hai số nguyên \(b,c\) mô tả một truy vấn (\(1 \le |b| \le 2 \times 10^9, 1 \le |c| \le 10^{18}\)).

Output

• Với mỗi truy vấn, đưa ra trên một dòng một số nguyên là kết quả của truy vấn đó.

Scoring

• Subtask \(1\) (\(20\%\) số điểm): \(n \le 10^3, q = 1\).
• Subtask \(2\) (\(20\%\) số điểm): \(|a_i| \le 10^6, |c| \le 10^9\).
• Subtask \(3\) (\(20\%\) số điểm): \(|c| \le 10^9\).
• Subtask \(4\) (\(20\%\) số điểm): \(a_i\) phân biệt từng đôi một.
• Subtask \(5\) (\(20\%\) số điểm): không có ràng buộc gì thêm.

Example

3
1 3 2
1
3 2

1

Hôm nay là ngày sinh nhật của Bob, mẹ của Bob tặng cho cậu một xâu \(s\). Thích thú với món quà trên tay, Bob liền chạy đi tìm Alice để chơi trò xoá xâu.

Luật chơi: Mỗi lượt, một người được chọn \(2\) kí tự liên tiếp giống nhau và xoá chúng ra khỏi xâu \(s\). Người nào không thực hiện được thao tác xoá sẽ bị xử thua.

Vì là xâu của Bob nên Bob đương nhiên sẽ được đi trước. Hãy tính toán xem nếu như Bob và Alice đều chơi tối ưu, thì ai sẽ là người chiến thắng?

Input

• Một dòng duy nhất là xâu \(s\) (Độ dài của xâu \(s \le 10^5\)) chỉ chứa các chữ cái từ a đến z.

Output

• Gồm một xâu duy nhất là Bob hoặc Alice tương ứng với người chiến thắng.

Scoring

• Subtask \(1\) (\(16\%\) số điểm): Xâu \(s\) chỉ chứa duy nhất một loại kí tự.
• Subtask \(2\) (\(84\%\) số điểm): không có ràng buộc gì thêm.

Example

abacaba

Alice

iiq

Bob

Có \(n\) học sinh đang xếp hàng từ trái sang phải. Mỗi học sinh được nhận diện bằng mã số sinh viên là \(ID\). Để thách đố học sinh của mình, thầy chủ nhiệm đã phát cho mỗi em học sinh một mảnh giấy để ghi lại mã số sinh viên lần lượt của bạn đứng trước (xếp bên trái) và sau đó là bạn đứng sau mình (xếp bên phải). Trong trường hợp không có bạn nào ở trước hoặc ở sau thì học sinh sẽ điền giá trị 0.

Sau khi đã viết lên giấy xong, thầy bắt đầu thu hồi lại các mảnh giấy và sắp xếp lại các mảnh giấy theo một trình tự ngẫu nhiên. Sau đó thầy hỏi các bạn về thứ tự xếp hàng ban đầu.

Cho dữ liệu về số học sinh \(n\) và nội dung theo đúng trình tự của các mảnh giấy. Hãy cho biết ban đầu, các học sinh đã xếp hàng như thế nào?

Input

• Dòng đầu tiên là số nguyên dương \(n\) (\(n \leq 2 \times 10^5\)) là số học sinh đã tham gia xếp hàng.
• \(n\) dòng tiếp theo: mỗi dòng là hai số nguyên dương \(a_{i}\) và \(b_{i}\) \((a_{i}, b_{i} \leq 10^6)\) lần lượt là \(ID\) của bạn đứng trước và \(ID\) của bạn đứng sau. Nếu \(a_{i} = 0\) thì không có bạn nào đứng trước và nếu \(b_{i} = 0\) thì không có bạn nào đứng sau.

Output

• Gồm \(n\) số nguyên dương là \(ID\) của các bạn theo trình tự xếp hàng ban đầu từ trái sang phải của các bạn học sinh.

Scoring

• Subtask \(1\) (\(20\%\) số điểm): \(n \leq 10\).
• Subtask \(2\) (\(80\%\) số điểm): Không ràng buộc gì thêm.

Example

5
1 3
0 5
5 2
3 4
2 0

1 5 3 2 4

Nem chua (phương ngữ Bắc Bộ) hay nem (phương ngữ Trung Bộ và phương ngữ Nam Bộ) là một món ăn sử dụng thịt lợn, lợi dụng men của lá chuối (hoặc lá ổi, lá vông, lá sung v.v.) và thính gạo để ủ chín, có vị chua ngậy. Nổi tiếng ở Việt Nam như một sản vật phổ biến tại nhiều địa phương, tuy không rõ nem chua được người dân vùng nào làm ra đầu tiên. Cách chế biến nem có thể chia thành hai kiểu: Nem Miền Bắc có thể chế biến ăn sống cùng các loại lá đặc biệt; còn Nem Miền Trung (đặc biệt Thanh Hoá và Huế) được đóng gói và lên men trong một số loại lá, trong đó có lá chuối, lá ổi.

Nem chua nên dùng sau khi lên men càng sớm càng tốt vì nếu để lâu thì nem chua sẽ bị thối rửa.

Một vị khách nước ngoài đang đi du lịch ở Việt Nam có dự định mua \(n\) cục nem chua chưa lên men để đem về nước. Nhưng anh ta không biết mua thế nào để ăn cho các ngày tiếp theo (mỗi ngày chỉ được ăn tối đa một cục nem) sao cho số nem bị thối rửa là ít nhất. May mắn thay, chủ tiệm là một người bán hàng có tâm nên đã liệt kê ra một danh sách gồm \(n\) cục nem. Mỗi cục nem sẽ lên men vào ngày thứ \(a_{i}\) và sẽ thối rửa sau ngày thứ \(b_{i}\). Với danh sách mà người bán hàng đã đưa, hãy tính toán số nem tối đa mà vị khách nước ngoài có thể ăn được sau khi đã đem về nước.

Input

• Dòng đầu tiên là số nguyên dương \(n\) (\(n \leq 10^5\)) là số cục nem định mua.
• \(n\) dòng tiếp theo gồm hai số nguyên dương \(a_{i}\) và \(b_{i}\) (\(a_{i} \leq b_{i} \leq 10^6\)). Với \(a_{i}\) là ngày cục nem thứ \(i\) lên men và \(b_{i}\) là ngày cục nem thứ \(i\) thối rữa.

Output

• Gồm một số nguyên duy nhất là số cục nem tối đa có thể ăn được nếu như vị khách cố gắng ăn tối ưu.

Scoring

• Subtask \(1\) (\(30\%\) số điểm): \(n\leq 10\) và \(a_{i}, b_{i} \leq 15\).
• Subtask \(2\) (\(40\%\) số điểm): \(n \leq 10^3\) và \(a_{i}, b_{i} \leq 10^3\)
• Subtask \(3\) (\(30\%\) số điểm): Không ràng buộc gì thêm.

Example

5
1 2
1 1
2 2
2 3
1 4

4

"Trong khoa học máy tính, cây là một tập hợp các nút được liên kết với nhau theo quan hệ cha-con. Vì tính chất mỗi nút con chỉ có một nút cha và tùy thuộc vào nút gốc được chọn trong cây mà mối quan hệ cha con này mới được hình thành. Hai nút có thể là cha con với nhau nếu như nút \(u\) được chọn làm nút gốc nhưng nếu ta chọn một nút \(v\) khác làm nút gốc thì tính chất này có thể sẽ bị đảo ngược lại và không được cố định..."

Tiếng giảng bài khô khan của thầy Tí truyền qua đầu Tí rồi tan vào hư vô. Suốt một buổi học kéo dài \(3\) tiếng về đồ thị, đọng lại trong Tí chỉ là một chữ "cây". Cây là gì? Tí không liệt môn Sinh mà ngược lại còn đạt giải học sinh giỏi quốc gia môn Sinh nữa. Không lẽ \(1\) cái cây mà Tí không biết nó là gì?

Trong sự bực bội, Tí lỡ tay làm rớt cây bút xuống đất. Cậu liền nhanh tay cúi xuống nhặt cây bút lên, xong cũng đưa cặp mắt lên bảng thật nhanh để thầy không chú ý. Nhưng kỳ lạ thay, cái bảng lúc nãy còn trống không bây giờ đã có một cái cây to đùng trên đó. Cây này nó rất lạ nhưng lạ hơn là có chữ "Bài tập về nhà".

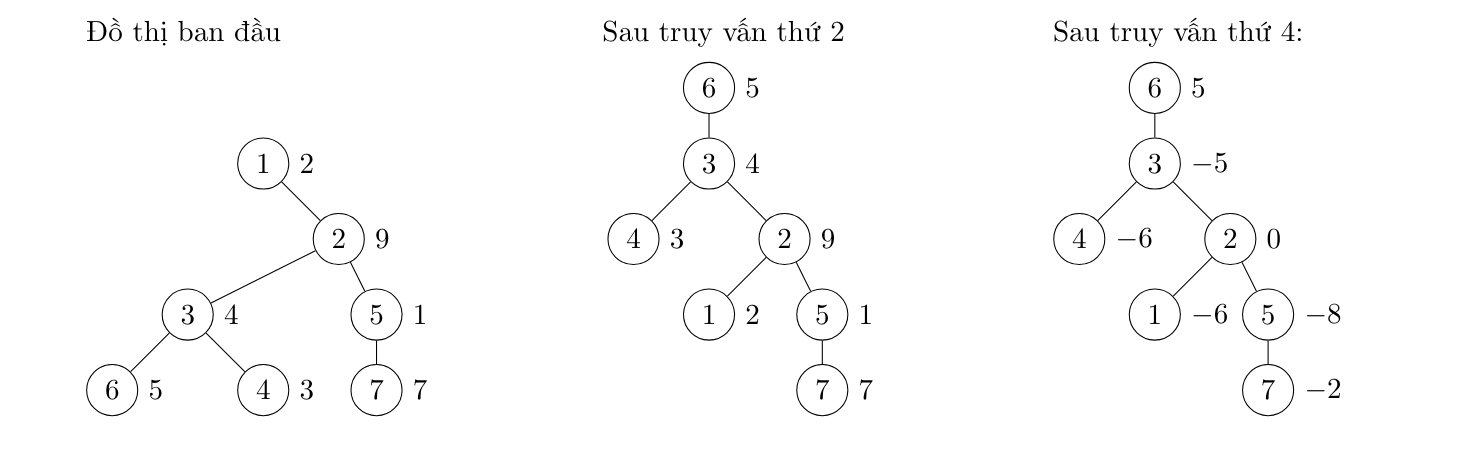
Cây trên bảng có \(n\) đỉnh và \(n - 1\) cạnh. Mỗi đỉnh \(i\) mang một giá trị \(v_{i}\). Bên dưới là \(q\) truy vấn liên quan đến cây được thầy Tí viết lên bảng như sau:

• \(1\) \(v\): đổi nút gốc của cây thành nút \(v\).
• \(2\) \(u\) \(v\) \(x\): Với mỗi nút trong cây con có độ lớn nhỏ nhất chứa cả nút \(u\) và \(v\). Hãy tăng giá trị của các nút trong cây con đó thêm \(x\).
• \(3\) \(v\): Tính tổng giá trị của cây con gốc \(v\).

Cây con của đỉnh \(v\) là tập hợp các đỉnh sao cho \(v\) nằm trên đường đi ngắn nhất từ đỉnh này đến gốc của cây.

Hãy giúp Tí giải bài tập về nhà của thầy cho.

Input

• Dòng đầu tiên gồm hai số nguyên dương \(n\) và \(q\) \((1 \leq n, q \leq 10^{5})\) lần lượt là số nút của cây và số truy vấn thầy Tí đưa.
• Dòng thứ hai gồm \(n\) số nguyên \(a_{1}, a_{2}, a_{3}, \ldots, a_{n}\) \((-10^{8} \leq a_{i} \leq 10^{8})\) là các giá trị ban đầu của các nút.
• \(n - 1\) dòng tiếp theo, môi dòng chứa hai số nguyên \(u\) và \(v\) \((1 \leq u, v \leq n, u \neq v)\) biểu diễn một cạnh của cây có nối từ đỉnh \(u\) tới đỉnh \(v\).
• \(q\) dòng tiếp theo biểu diễn các truy vấn, mỗi truy vấn thuộc một trong ba dạng như sau:
  • \(1\) \(v\) (\(1 \le v \le n\)): Thể hiện truy vấn loại \(1\).
  • \(2\) \(u\) \(v\) \(x\) (\(1 \le u,v \le n, -10^8 \le x \le 10^8\)): Thể hiện truy vấn loại \(2\).
  • \(3\) \(v\) (\(1 \le v \le n\)): Thể hiện truy vấn loại \(3\).

Output

• Với mỗi truy vấn loại \(3\), in ra một dòng là kết quả của truy vấn đó.

Scoring

• Subtask \(1\) (\(15\%\) số điểm): \(n, q \leq 5000\).
• Subtask \(2\) (\(15\%\) số điểm): mỗi đỉnh có tối đa hai cạnh kết nối với đỉnh đó.
• Subtask \(3\) (\(15\%\) số điểm): không có truy vấn loại \(1\).
• Subtask \(4\) (\(15\%\) số điểm): không có truy vấn loại \(2\).
• Subtask \(5\) (\(20\%\) số điểm): trong các truy vấn loại \(2\): \(u = v\).
• Subtask \(6\) (\(20\%\) số điểm): không có rằng buộc gì thêm.

Example

7 5
2 9 4 3 1 5 7
1 2
2 3
2 5
3 4
3 6
5 7
3 3
1 6
3 2
2 1 4 -9
3 5

12
19
-10