Tin học trẻ quận Sơn Trà - 2023 (Bảng A)

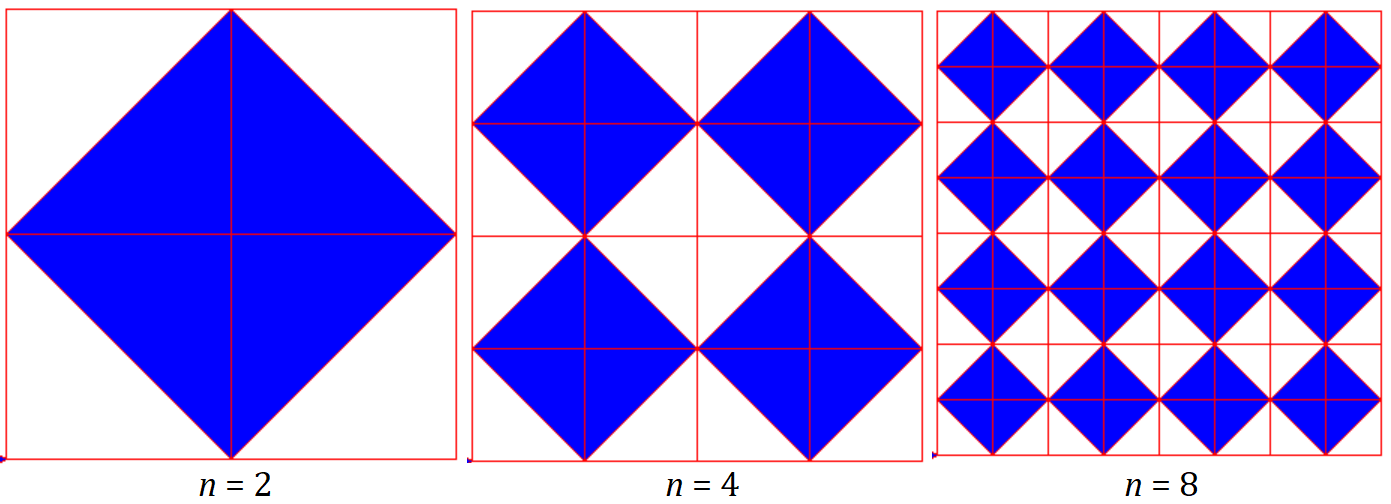
NMột mảng tường vuông có kích thước \(n×n\) hình vuông đơn vị (với \(n\) là số chẵn) được trang trí hoa văn sau:

Yêu cầu: Nhập vào số tự nhiên chẵn \(n\ (2≤n≤10)\), hãy vẽ mảng tường \(n×n\) tương ứng.

Chú ý:

• Tô màu có dạng giống hình vẽ, có thể thay màu khác.
• Không sử dụng nhân vật giống hình vẽ.

Chấm điểm: Vẽ được hình vuông đúng mà không tô màu thì trừ 40% số điểm của mỗi trường hợp tương ứng.

Bạn được đưa cho một tấm bảng hình chữ nhật gồm \(M×N\) ô vuông. Ngoài ra, bạn được cung cấp một số lượng không giới hạn quân cờ domino tiêu chuẩn có kích thước \(2 × 1\) (các quân cờ được phép xoay 90 độ). Bạn được yêu cầu đặt càng nhiều quân cờ domino càng tốt trên bảng sao cho đáp ứng các điều kiện sau:

• Mỗi quân domino bao hoàn toàn 2 hình vuông trên bảng.
• Không có 2 quân domino nào đè lên nhau hay mỗi ô trên bảng được lấp bởi tối đa 1 quân domino.
• Mỗi quân domino nằm hoàn toàn bên trong bàn cờ. Nó được phép chạm vào các cạnh của bảng.

Yêu cầu: Tìm số quân cờ domino tối đa có thể đặt được thỏa mãn các điều kiện trên.

Dữ liệu:

• Dòng đầu tiên chứa số tự nhiên \(M\ (1≤M≤1 000)\).
• Dòng thứ hai chứa số tự nhiên \(N\ (1≤N≤1 000)\).

Kết quả: In ra một số tự nhiên duy nhất là số quân cờ domino tối đa có thể đặt được.

Scoring

• Subtask \(1\) (\(60\) điểm): \(M * N \leq 40\).
• Subtask \(2\) (\(40\) điểm): Không có ràng buộc gì thêm.

Example

2 
4

4

3 
3

4

Xâu giống nhau là xâu chỉ chứa một loại ký tự bất kỳ.

Bạn có được “phép thuật” lấy hai ký tự \(A,B\) bất kỳ để biến thành một ký tự \(C\).

Ví dụ: Xâu \(ABC\) có thể biến đổi thành xâu \(CC\)

Yêu cầu: Cho xâu \(S\) chỉ gồm ba ký tự \(A,B,C\), bạn có thể biến đổi thành xâu giống nhau hay không?

Dữ liệu: Một xâu ký tự \(S\) chỉ gồm ba ký tự \(A,B,C\) có độ dài không qua 1 000 ký tự.

Kết quả: In ra chữ YES nếu biến đổi xây \(S\) thành xâu giống nhau, ngược lại in chữ NO

Example

CCCB

NO

AAABBCB

YES

Note

• Ở test 2 đáp án là CCCC

Nam là nhà khảo cổ học, anh đã thăm dò và phát hiện nhiều cổ vật rất có giá trị. Để dễ quản lí các cổ vật, anh ta đánh số thứ tự cho các cổ vật, có \(n\) cổ vật được đánh số \(1, 2, 3, ... n\). Nam muốn biết với n cổ vật thì tổng các chữ số dùng để đánh số thứ tự là bao nhiêu?

Ví dụ: Có \(n=12\) cổ vật thì tổng các chữ số để đánh số thứ tự là : \(1+2+3+4+5+6+7+8+9+1+0+1+1+1+2=51\)

Yêu cầu Cho giá trị \(n\), hãy tính tổng các chữ số dùng cho việc đánh số thứ tự \(n\) cổ vật

Dữ liệu: Một số tự nhiên \(n\ (n≤10^{12})\).

Kết quả: Một số tự nhiên duy nhất là tổng các chữ số dùng để đánh số thứ tự của \(n\) cổ vật.

Scoring

• Có 60% số điểm của bài toán với \(n≤1 000 000\).
• Có 40% số điểm của bài toán với \(1 0000 000≤n≤10^{12}\).

Example

12

51

8

36