Sinh nhật LQDOJ 2023 - Contest ôn tập THT bảng C1 - 2023 #02

Chỉ còn không lâu nữa sẽ đến ngày mà bé Đôn tròn 3 tuổi. Vì bé Đôn là một cậu bé không những hoà đồng mà còn tốt bụng nên Lê và Quý muốn tổ chức một ngày sinh nhật thật hoành tráng cho cậu, trong đó Lê đảm nhận việc mua đồ trang trí.

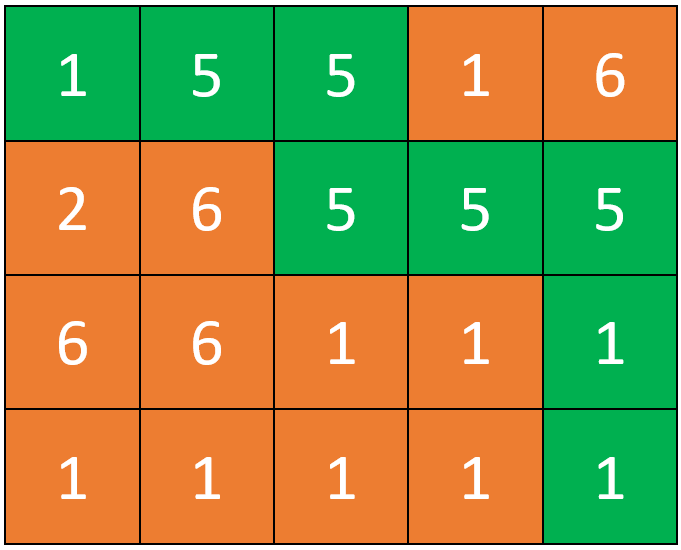
Khu vực bày bán đồ trang trí ở trung tâm mua sắm C giấu tên bao gồm \(n\) gian hàng, được đánh số từ \(1\) đến \(n\) theo thứ tự từ trên xuống dưới. Mỗi gian hàng có \(m\) món đồ trang trí, được đánh số từ \(1\) đến \(m\) theo thứ tự từ trái sang phải. Tuy nhiên, không phải món đồ nào cũng đẹp hay sặc sỡ giống nhau, thay vào đó món đồ thứ \(j\) ở gian hàng \(i\) sẽ có độ sặc sỡ là \(a_{ij}\). Độ sặc sỡ của một nhóm món đồ nào đấy sẽ là giá trị trung vị của nhóm này.

Hiện tại Lê đang đứng ở món đồ đầu tiên của gian hàng thứ nhất. Vì không có nhiều thời gian, Lê muốn mua hàng nhanh nhất có thể. Khi đến vị trí một món đồ nào đó, Lê sẽ lấy luôn món đồ này. Ngoài ra, Lê chỉ muốn di chuyển đi xuống hoặc sang phải và anh sẽ chỉ rời khỏi khu vực bày bán đồ trang trí này sau lấy được món đồ thứ \(m\) của gian hàng thứ \(n\). Hãy giúp Lê tìm lộ trình mua hàng sao cho độ sặc sỡ của toàn bộ số món đồ Lê mua là lớn nhất.

Ta xác định giá trị trung vị của một tập hợp số \(a_1, a_2, \ldots, a_n\) bằng cách sắp xếp tập hợp này theo thứ tự không giảm và chọn \(a_{\lfloor (n + 1)/2 \rfloor}\) là giá trị trung vị.

Input

• Dòng đầu tiên chứa hai số nguyên \(n\) và \(m\) (\(1 \leq n,m \leq 10^3\)) lần lượt là số gian hàng và số món đồ ở mỗi gian hàng.
• Trong \(n\) dòng tiếp theo, dòng thứ \(i\) chứa \(m\) số nguyên \(a_{ij}\) (\(0 \leq a_{ij} \leq n \times m\)) là độ sặc sỡ của món đồ thứ \(j\) của gian hàng \(i\).

Output

• Một số nguyên duy nhất là độ sặc sỡ lớn nhất tìm được.

Scoring

• Subtask \(1\) (\(30\%\) số điểm): \(n, m \leq 10\).
• Subtask \(2\) (\(30\%\) số điểm): \(n = 1\).
• Subtask \(3\) (\(40\%\) số điểm): Không có ràng buộc gì thêm.

Example

4 5
1 5 5 1 6
2 6 5 5 5
6 6 1 1 1
1 1 1 1 1

5

Trong khi Lê mua đồ trang trí thì Quý đi mua bánh sinh nhật. Sau khi dạo vòng quanh thành phố thì Quý đã tìm được một chiếc bánh ưng ý trong một cửa hàng. Tình cờ thay hôm nay cũng là ngày kỉ niệm 3 năm khai trương ở đây. Khách hàng nào mua bánh kèm với nến mà thoã mãn cả hai điều kiện sau thì sẽ được luôn tặng bánh (chỉ cần trả tiền nến):

• Tổng các chữ số của số lượng nến nằm trong khoảng từ \(L\) đến \(R\);
• Nếu xếp những cây nến đó thành các vòng tròn trên bánh, mỗi vòng tròn có đúng \(M\) cây nến cho đến khi không xếp được nữa thì còn dư đúng \(K\) cây nến để xếp ở giữa.

Hãy giúp Quý tìm số lượng nến ít nhất cần mua để có được khuyến mãi hoặc thông báo rằng cửa hàng đang lừa đảo vì không tồn tại cách mua.

Input

• Dòng đầu tiên chứa số nguyên \(t\) (\(1 \leq t \leq 10\)) là số lượng trường hợp cần kiểm tra.
• Trong \(t\) dòng tiếp theo, mỗi dòng chứa bốn số nguyên \(L\), \(R\), \(M\) và \(K\) (\(1 \leq L \leq R \leq 10^3\), \(0 \leq K < M \leq 10^3\)).

Output

• Ứng với mỗi trường hợp, in ra một số nguyên là số lượng nến ít nhất cần mua hoặc \(-1\) nếu không tồn tại cách mua.

Scoring

• Subtask \(1\) (\(20\%\) số điểm): \(M = 1\).
• Subtask \(2\) (\(20\%\) số điểm): \(R = 1\).
• Subtask \(3\) (\(30\%\) số điểm): \(L = R\).
• Subtask \(4\) (\(30\%\) số điểm): Không có ràng buộc gì thêm.

Example

5
5 7 1 0
1 1 6 4
7 7 8 2
2 3 3 1
1 10 134 47

5
10
34
-1
181

Sau nhiều ngày kỳ công chuẩn bị, sinh nhật hoành tráng và bùng nổ nhất của Đôn cuối cùng cũng diễn ra. Cậu đã nhận được rất nhiều lời chúc và đương nhiên là rất nhiều món quà. Trong số đó, nổi bật hơn cả chính là món quà của thầy Nhỏ. Tuy tên thầy là Nhỏ nhưng món quà thầy dành cho Đôn không hề nhỏ một chút nào. Món quà gồm có \(n\) món đồ chơi đánh số từ \(1\) tới \(n\). Đồ chơi thứ \(i\) có độ yêu thích \(a_i\). Các đồ chơi được nối với nhau bằng \(n-1\) sợi dây kim tuyến sặc sỡ, trong đó sợi dây thứ \(i\) nối đồ chơi thứ \(u_i\) và \(v_i\) với nhau.

Tuy nhiên, đâu phải dễ dàng gì mà được nhận quà của thầy Nhỏ. Thầy sẽ cắt từ món quà của mình một "đoạn" đồ chơi và dây kim tuyến sao cho "đoạn" này hoặc chỉ gồm một món đồ chơi duy nhất, hoặc có thể duỗi thành một đường thẳng có đầu thứ nhất là đồ chơi thứ \(s_i\), đầu thứ hai là đồ chơi thứ \(t_i\), ở giữa là không, một hoặc một số món đồ chơi khác và giữa hai đồ chơi liền kề có một dây kim tuyến. Sau khi thầy cắt xong, Đôn sẽ được bỏ đi một số đồ chơi kề nhau tùy ý ở hai đầu của "đoạn" vừa cắt (có thể không bỏ đồ chơi nào hoặc bỏ tất cả) và nhận về toàn bộ các đồ chơi còn lại trong "đoạn".

Với mỗi cách cắt của thầy Nhỏ, hãy giúp Đôn bỏ đi một số đồ chơi sao cho tổng độ yêu thích của các đồ chơi Đôn nhận được là lớn nhất.

Dữ liệu đảm bảo giữa hai đồ chơi khác nhau bất kỳ tồn tại đúng duy nhất một "đoạn" đồ chơi và dây kim tuyến có hai đầu là hai đồ chơi này.

Input

• Dòng đầu tiên chứa hai số nguyên \(n\) và \(q\) (\(1 \leq n, q \leq 2 \cdot 10 ^ 5\)) lần lượt là số lượng món đồ chơi và số lượng cách cắt của thầy Nhỏ.
• Dòng tiếp theo chứa \(n\) số nguyên \(a_1, a_2, \ldots, a_n\) (\(|a_i| \leq 10 ^ 9\)) là độ yêu thích của các món quà.
• Trong \(n - 1\) dòng tiếp theo, dòng thứ \(i\) chứa hai số nguyên \(u_i\) và \(v_i\) (\(1 \leq u_i, v_i \leq n\)) cho biết dây thứ \(i\) nối đồ chơi thứ \(u_i\) và \(v_i\) với nhau.
• Trong \(q\) dòng tiếp theo, dòng thứ \(i\) chứa hai số nguyên \(s_i\) và \(t_i\) (\(1 \leq s_i, t_i \leq n\)) mô tả một cách cắt của thầy Nhỏ.

Output

• Ứng với mỗi cách cắt, in ra một số nguyên là độ yêu thích lớn nhất của các đồ chơi Đôn nhận được.

Scoring

• Subtask \(1\) (\(15\%\) số điểm): Mỗi món đồ chơi nối với không quá \(2\) món đồ chơi khác và \(n, q \leq 2 \cdot 10 ^ 2\).
• Subtask \(2\) (\(15\%\) số điểm): Mỗi món đồ chơi nối với không quá \(2\) món đồ chơi khác và \(n, q \leq 2 \cdot 10 ^ 3\).
• Subtask \(3\) (\(20\%\) số điểm): Mỗi món đồ chơi nối với không quá \(2\) món đồ chơi khác.
• Subtask \(4\) (\(15\%\) số điểm): \(n, q \leq 2 \cdot 10 ^ 2\).
• Subtask \(5\) (\(15\%\) số điểm): \(n, q \leq 2 \cdot 10 ^ 3\).
• Subtask \(6\) (\(20\%\) số điểm): Không có ràng buộc gì thêm.

Example

5 3
4 -3 -2 5 -1
1 2
1 3
2 4
2 5
3 4
5 3
2 5

6
4
0

Sau một ngày ăn chơi sinh nhật hết mình, Đôn về nhà và liền leo lên giường. Đột nhiên Đôn nhớ lại mình chưa làm bài tập môn Bitwise 101 dành cho trẻ mầm non. Đề bài ấy như sau:

Đôn vì chơi sinh nhật quá hăng nên giờ chẳng còn tí sức nào để làm bài nữa. Hãy giúp Đôn nhé.

Input

• Dòng đầu tiên chứa số nguyên \(n\) (\(1 \leq n \leq 10^6\)) là số lượng phần tử trong dãy.
• Dòng tiếp theo chứa \(n\) số nguyên \(a_1, a_2, \ldots, a_n\) (\(0 \leq a_i \leq 10^6\)) là giá trị của các phần tử trong dãy.

Output

• Một số nguyên duy nhất là độ dài dãy con là dãy tốt dài nhất.

Scoring

• Subtask \(1\) (\(20\%\) số điểm): \(a_i \leq 1\).
• Subtask \(2\) (\(10\%\) số điểm): \(n \leq 10^2\).
• Subtask \(3\) (\(10\%\) số điểm): \(n \leq 10^3\).
• Subtask \(4\) (\(60\%\) số điểm): Không có ràng buộc gì thêm.

Example

3
1 0 1

0

2
5 6

2

6
8 1 3 3 1 2

4