Giao lưu Tin học trẻ Mở rộng Bảng A - Lần 2 - 2023

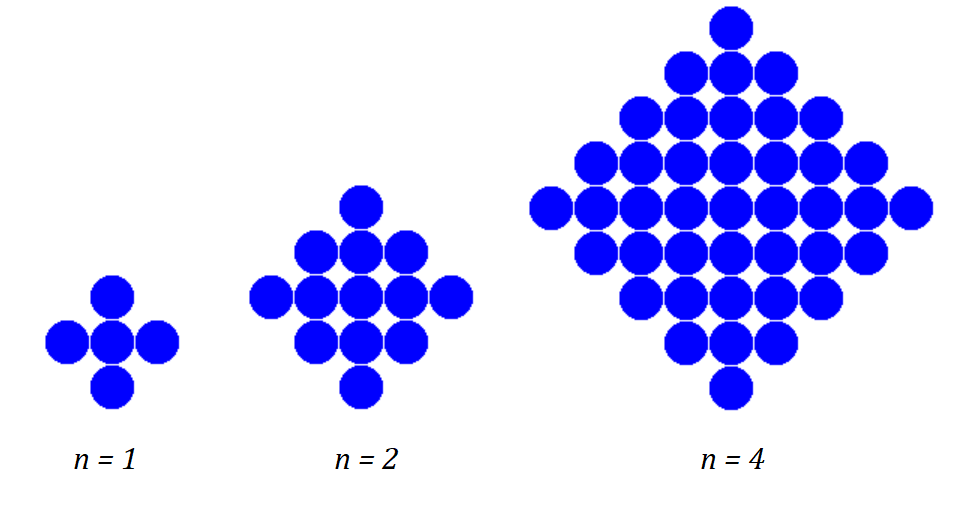
Các hình tròn được sắp xếp theo cách sau: Ban đầu có 1 hình tròn ở giữa tâm màn hình gọi là bậc 0. Bậc 1 là xếp thêm 1 lớp 4 hình tròn vào 4 hướng của hình tròn ban đầu. Bậc 2 là xếp thêm lớp tiếp theo vào hình bậc 1, ...

Yêu cầu: Nhập vào số tự nhiên \(n\) (\(1 \le n \le 10\)), hãy vẽ ra hình bậc \(n\) tương ứng:

Bài vẽ hình chưa chấm tự động được nên các em sẽ nộp file lên Google Drive theo link sau và sẽ được chấm sau:

• Đặt tên file là Tên TK _ Bai1 ** như **Small_Bai1

https://docs.google.com/forms/d/e/1FAIpQLSfnXg8rRqr6gIjxdEO4m8zKdm7Z9IHAnkIQIeHaHG1lAfZjyQ/viewform

Cho một xâu \(s\) có độ dài \(n\)(\(n\) chẵn) chỉ bao gồm các chữ cái Latin viết hoa '\(A\)', '\(B\)' và '\(C\)'. Mỗi lượt bạn có thể thực hiện một trong hai hành động sau:

• Bạn có thể xóa chính xác một chữ cái '\(A\)' và chính xác một chữ cái '\(B\)' khỏi các vị trí tùy ý của chuỗi (các chữ cái này không nhất thiết phải liền kề nhau);
• Hoặc bạn có thể xóa chính xác một chữ cái '\(B\)' và chính xác một chữ cái '\(C\)' khỏi các vị trí tùy ý của chuỗi (các chữ cái này không nhất thiết phải liền kề nhau).

Do đó, độ dài của xâu giảm đi đúng một lượng là 2 chữ cái. Tất cả các lượt đều độc lập nên đối với mỗi lượt, bạn có thể chọn bất kỳ hành động nào trong hai hành động có thể.

Ví dụ, với \(s\) = "\(ABCABC\)" anh ta có thể nhận được một xâu \(s\) = "\(ACBC\)" trong một lượt (bằng cách xóa lần xuất hiện đầu tiên của '\(B\)' và lần xuất hiện thứ hai của '\(A\)'). Ngoài ra còn có nhiều tùy chọn khác để thực hiện ngoài ví dụ cụ thể này.

Với xâu kí tự \(s\) đã cho bạn có thể xác định rằng liệu có cách thực hiện các thao tác trên để biến xâu \(s\) thành rỗng hay không. Nếu có thì in ra 'YES' còn không có thì in ra 'NO'.

Input

• Dòng đầu tiên chứa 2 số nguyên dương \(n\). \((1 \leq n \leq 100000)\) - thể hiện chiều dài của xâu.
• Dòng thứ 2 chứa xâu \(s\).

Output

• Một dòng duy nhất là 'YES' hoặc 'NO' tương ứng là có hoặc không có cách thực hiện các thao tác đã cho để biến xâu \(s\) thành rỗng.

Example

6
ABACAB

NO

16
BCBCBCBCBCBCBCBC

YES

Doraemon và Nobita đang cắm trại trên vùng đất là một hệ tọa độ Descartes. Doraemon thử tài Nobita bằng cách giấu kho báu tại một tọa đồ
bất kỳ, và Nobita sẽ là người đi tìm.

Ban đầu cả hai đang ở tọa độ \((0, 0)\) và Doraemon sẽ bắt đầu đi giấu kho báu.

Tại tọa độ \((x, y)\) bất kỳ, trong một bước đi Doraemon sẽ đi tới một trong bốn tọa độ là:

• \((x + 1, y)\): Đi qua bên phải;
• \((x, y + 1)\): Đi lên phía trên;
• \((x − 1, y)\): Đi qua bên trái;
• \((x, y − 1)\): ĐI xuống phía dưới.

Quay về sau một khoảng thời gian, Doraemon nói với Nobita rằng mình không đi quá \(N\) bước từ vị trí bắt đầu để đi giấu kho báu, và có thể giấu kho báu ngay tại vị trí \((0, 0)\) trong lúc Nobita không để ý.

Nobita muốn biết trong trường hợp xấu nhất, mình phải đến bao nhiêu vị trí để tìm thấy được kho báu, tính luôn vị trí ban đầu.

Ví dụ:

• Với \(n=1\) thì có 5 chỗ giấu kho bấu được đánh dấu x
• Với \(n=2\) thì có 13 chỗ giấu kho bấu được đánh dấu x

Dữ liệu

• Một dòng duy nhất bao gồm 1 giá trị \(N\)

Kết quả

• Gồm một số nguyên duy nhất là số vị trí nhiều nhất mà Anh cần phải tới.

Scoring

• \(0 ≤ N ≤ 10^5\).
• \(0 ≤ N ≤ 10^9\).

Example

1

5

Có một loài Rùa có cách di chuyển kì lạ. Sau khi di chuyển tới \(i\) bước thì lại di chuyển lùi từ 1 đến \(i\) bước. Nghĩa là lượt hiện tại di chuyển tới thì lượt sau di chuyển lùi và ngược lại.

Lưu ý: Sau mỗi lần di chuyển tới thì \(i\) tăng dần đều 1 đơn vị, khởi đầu là 1.

Yêu cầu: Quãng đường có độ dài là \(N\) đơn vị. Hỏi Rùa phải di chuyển tối thiểu bao nhiêu lượt mới đến đích.

Ví dụ: Với \(N=3\) thì các lần di chuyển của Rùa như sau:

• Lần 1: Di chuyển lên \(i=1\) đơn vị, đi được quãng đường 1 đơn vị
• Lần 2: Di chuyển lùi 1 đơn vị, quay về vị trí khởi đầu
• Lần 3: Di chuyển lên \(i=2\) đơn vị, đi được quãng đường 2 đơn vị (\(i\) tăng lên 1 đơn vị)
• Lần 4: Di chuyển lùi 2 đơn vị, quay về vị trí khởi đầu
• Lần 5: Di chuyển lên \(i=3\) đơn vị, đã đi đến đích (\(i\) tăng lên 1 đơn vị)

Vậy sau 5 lần di chuyển, Rùa đã di chuyển đến đích

Input

• Nhập số tự nhiên \(N\) với \(1 \le N \le 10^{15}\).

Output

• Xuất ra số lần di chuyển tối thiểu của Rùa.

2

3

3

5