10^6, 10^7 và những người bạn Div 3

Tấn đang tham gia một cuộc thi coding tập thể. Trong team của Tấn có \(n\) người, mỗi người có chỉ số không ăn hại là \(A_i\) \((|A_i|\le 100 )\). Chỉ số càng thấp thì độ không ăn hại càng thấp, tức là họ sẽ càng ăn hại. Độ không ăn hại của đội được tính là tích của tất cả các chỉ số không ăn hại của toàn team. Tấn muốn bỏ bớt một số người để độ không ăn hại của đội càng cao càng tốt. Hãy giúp Tấn biết cần loại bỏ ít nhất bao nhiêu người, sao cho độ không ăn hại của đội cao nhất có thể.

Input

• Dòng 1 gồm số \(n(n\le 100)\)
• Dòng 2 gồm \(n\) số nguyên của dãy \(A\)

Output

• In ra \(1\) số là số người ít nhất cần loại bỏ

Example

3
-1 2 4

1

4
-1 -1 -1 4

1

Sau khi cắn rứt bỏ đi các bạn của minh, Tấn đã có thể yên tâm tham gia cuộc thi ấy. Bài đầu tiên được team phân công cho Tấn ở vòng \(I\) là \(1\) bài dễ ơi là dễ, cụ thể như sau:

Bạn có \(1\) dãy số \(A\) có \(n\) số \(0\). Bạn được cho thêm \(1\) dãy số nguyên dương \(B\) cũng có \(n\) phần tử với các \(B_i\le 1000\). Bạn có thể chọn tăng thêm \(1\) cho \(2\) phần tử bất kỳ(có thể trùng nhau). Hãy cho biết có thể biến đổi dãy \(A\) thành dãy \(B\) được không? In YES / NO để trả lời.

Cậu ấy thấy bài đó có vẻ quá dễ nên đã bỏ qua không làm bài này và cái kết để bài ấy còn có 1p để làm. Bạn ấy quá hoảng loạn nên không biết làm gì, các bạn hãy giúp anh bạn ấy nhé.

Input

• Dòng 1 gồm số \(n(n\le 100)\)
• Dòng 2 gồm \(n\) số nguyên của dãy \(B\)

Output

• In ra YES / NO.

Example

3
1 1 2

YES

Sau khi hú vía mới qua được cảnh ngàn cân treo sợi tóc ấy, Tấn đã thành công đưa team chiếm giải kk và mới được ba tặng con Robot siêu cấp có cục pin siêu khủng. Tấn hằng ngày vẫn lấy nó ra chơi. Cho đến \(1\) ngày, Tấn đọc được bài viết về Tỉ Lệ Vàng, Tấn mới nghĩ ra một trò chơi mới.

Tấn lôi cái bàn cờ vô hạn của mình ra, và đánh dấu \(T\) khu vực hình chữ nhật, khu thứ \(i\) có \(2\) cạnh lần lượt là \(X_i\) và \(Y_i\). Với mỗi khu thứ \(i\), Tấn đặt con Robot lên ô trái trên của khu vực ấy, đặt \(1\) cây bút màu mà cậu dùng để đánh dấu khu vực xuống phía dưới con Robot cho nó vạch đường đi, rồi chơi như sau: Hướng góc nhìn của cả con Robot về hướng bên tay phải, rồi cho nó di chuyển liên tục. Nếu như ô nó dự định đi tới (hoặc \(1\) cạnh kề ô đó) bị vẽ màu thì nó sẽ dừng lại, nó sẽ quay \(90^o\) về phía tay phải (so với góc nhìn của con robot) rồi đi tiếp. Cho đến \(1\) ô nào đó mà nó quay đủ \(360^o\) mà không thể tìm thấy đường đi hợp lệ thì nó sẽ dừng lại và báo hiệu cho Tấn biết số hiệu của ô nó dừng lại:

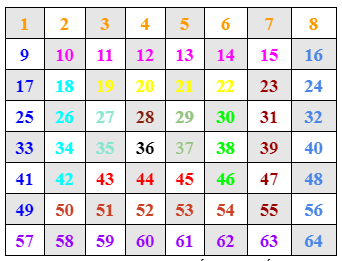
Các ô được đánh số như thế này trong khu vực \(8\times 8\). Robot sẽ từ ô số \(1\) qua ô số \(8\) (hàng số màu cam), rồi từ đó đi đến ô số \(64\) (hàng số màu xanh nhạt), rồi từ đó đi tiếp đến ô \(57\) (hàng số màu tím), rồi tới ô số \(9\) (hàng số màu xanh đậm), rồi tiếp tục quay rồi đi tiếp tới ô \(15\) (hàng số màu hường), rồi đi tiếp… cho đến ô số \(36\) (ô in đậm) thì Robot không tìm thấy đường đi nên nó sẽ dừng.

Cậu ghi lại ô dừng của Robot trong \(T\) trường hợp, rồi đem cho Tài xem. Mỗi tội sau đó Tấn lại lỡ tay làm rách tờ giấy nên kết quả cậu ghi lại đều bị mất hết, may thay vẫn còn các giá trị \(X_i\) và \(Y_i\) của \(T\) khu vực ấy, nên ít nhất cậu cũng hy vọng có thể khôi phục lại kết quả. Các bạn ơi, hãy giúp Tấn tìm ra các kết quả bị mất nhé!

Input

• Dòng 1 gồm số \(T\le 10^3;\)
• \(T\) dòng sau, mỗi dòng thứ \(i\) có \(2\) số \(X_i\) và \(Y_i\) \((X_i,Y_i\le 10^3).\)

Output

• Với mỗi dòng thứ i, in ra theo đề yêu cầu (kèm chữ “Test #” với chỉ số của câu hỏi (i).

Scoring

• Subtask #1 (\(20\%\) số điểm): \(X_i,Y_i \le 10.\)
• Subtask #2 (\(50\%\) số điểm): \(X_i,Y_i \le 10^2.\)
• Subtask #3 (\(30\%\) số điểm): Không có ràng buộc gì thêm

Example

1
8 8

Test #1: 36

Tấn mới mua giấy màu về để làm thủ công \(3D\) với Trinh. Nhưng hai bạn mua hơi bị nhiều giấy nên sau khi làm xong giấy vẫn chất đống. Trinh chưa biết làm gì với đống giấy thừa ấy thì Tấn lấy một mảnh giấy hình chữ nhật ra gấp đôi lại. Nào, không phải gấp đôi theo chiều ngang hay dọc đâu, mà là theo đường chéo nhé. Tấn nhìn thấy thế liền nói: Này, thế diện tích cái hình cậu mới gấp lại là bao nhiêu vậy? Trinh bí, cô không giỏi Toán hình lắm, nên cậu nhờ các bạn rằng: Nếu Tấn gấp \(Q\) tờ giấy chữ nhật, mỗi tờ thứ \(i\) có \(2\) cạnh là \(a_i(cm)\) và \(b_i(cm)\), thì diện tích hình vừa tạo ra là bao nhiêu \(cm2\) ??? Nói tóm lại, hãy điền vào câu sau:

Cho hình chữ nhật có kích thước \(a * b\), diện tích hình gấp được là ………

VD (hình ABEFC là kết quả của hình gấp hình chữ nhật kích thước \(2 * 3\)):

Các kết quả được làm tròn tối đa 10 chữ số thập phân.

Input

• Dòng \(1\) gồm số \(Q\)
• \(Q\) dòng tiếp theo, mỗi truy vấn thứ \(i\) gồm số \(a_i, b_i.\)

Output

• Với mỗi truy vấn, in ra theo đề yêu cầu.

Example

1
1 1

0.5cm2

Giới hạn: \(Q≤10^3;\) \(a_i, b_i≤10^5.\)

Subtask:

• 30% số test có các \(a_i=b_i.\)

Một số \(n\) bất kì luôn có \(1\) tập ước số không chứa \(1\) riêng của nó, dù là số nguyên tố hay hợp số. Ví dụ như số \(6\) có tập ước số không chứa \(1\) là \((2;3;6)\), còn số \(420\) có tập ước số không chứa \(1\) là \((2;3;4;5;6;7;10;12;14;15;20;21;28;35;60;84;105;140;210;420)\). Trinh mới học thêm về số nguyên tố và hợp số, liền về nhà lấy giấy ra viết \(1\) số \(420\) và dãy ước không chứa \(1\) của chính số \(420\) ấy. Viết xong rồi, cậu nhìn lại thì thắc mắc: Ủa? Sao có nhiều đoạn số liên tiếp thế này? Có đoạn có tới \(6\) số liên tiếp lận? (Nếu bạn thắc mắc là đoạn nào, thì đó là đoạn \((2;3;4;5;6;7)\) đấy) Rồi cô nghĩ tiếp: Thế nếu mình muốn tạo ra \(1\) số \(n\) bất kì mà trong dãy ước ấy có ít nhất \(1\) đoạn liên tiếp có \(k\) số thì làm thế nào nhỉ? Cô bí bài này nên cô muốn nhờ các bạn ở LQDOJ rằng: Cho \(1\) số tự nhiên \(k(k\le 100)\), hãy tìm số nguyên dương \(n\) bé nhất có thể mà trong dãy ước số không chứa \(1\) của nó có ít nhất \(1\) đoạn số liên tiếp có chiều dài không nhỏ hơn \(k\).

Input

• Duy nhất \(1\) số \(k\)

Output

• Ans mod cho \(10^9+7\).

Example

2

6