10^6, 10^7 và những người bạn Div 1

Fibonacci là một dãy số huyền bí được phát minh ra từ xa xưa, là nghiệm của \(1\) bài toán ít người biết đến trong bộ sách … gì gì đó ko nhớ nữa :))) . Những con số đầu tiên của dãy là \((1;1;2;3;5;8; ...)\). Trinh rất thích dãy số này, và thường xuyên cho Tấn xem những gì cô mới chơi đùa được với dãy số ấy. Tấn cũng đã học về dãy số ấy và phát hiện nó có một điều gì đó rất bất bình thường. Sau một hồi khám phá, cuối cùng mọi thứ được đúc kết trong câu đố của cậu cho Trinh:

Cho \(T\) số \(n\). Với mỗi số \(n\), tìm tổng các ước số của số Fibonacci thứ \(n\) mà nó là số Fibonacci, sao cho các ước không được trùng nhau (\(2\) số \(1\) đầu dãy được tính làm \(1\)).

Trinh, dù thích câu đố này, nhưng không thể làm nó vì cô đang bận xem bóng đá Vòng Loại thứ \(3\) World Cup khu vực Châu Á (hay ít nhất là cô nói với cậu thế). Trinh nhờ các bạn giải giúp câu đố này.

Nhưng mọi chuyện vẫn chưa kết thúc tại đây. Tấn còn ác hơn khi cho các số \(n\) của cậu ẩn trong \(1\) xâu kí tự \(S\), trong đó các số \(n\) được bao giữa các dấu ngoặc tròn “( )”, và số \(T\) của cậu bị ẩn và bạn sẽ chẳng biết được số \(T\) này. Mục đích của việc này là làm cho các bạn loạn mắt lên thôi chứ chẳng có gì cả :))) Trinh “trả giá” độ khó bài này vì các bạn và cuối cùng Tấn chỉ cho thêm \(1\) cái điều kiện “giảm bớt” là: Các cặp ngoặc không lồng vào nhau, chúng độc lập với nhau và không tác động lên các cặp ngoặc kia. Trinh đành chấp nhận thử thách của cậu và nhờ các bạn. Các bạn hãy giúp Trinh nhé 🙁 Các kết quả của cùng 1 số n in ra mỗi kết quả mỗi dòng.

Input

• Gồm \(1\) dòng duy nhất là xâu \(S\), chứa \(T\) số \(n\) (\(T\) ẩn và \(T≤100\) cùng với các \(n≤10^{12}\)).

Output

• Với mỗi số \(n\), mỗi dòng in \(1\) kết quả là tổng các ước số của số Fibonacci thứ n mà nó là số Fibonacci sau khi mod \(10^9+7\).

Scoring

• Subtask \(1\) (\(25\%\) số điểm): \(n≤10^3.\)
• Subtask \(2\) (\(25\%\) số điểm): \(n≤10^6.\)
• Subtask \(3\) (\(25\%\) số điểm): \(n≤10^9.\)
• Subtask \(4\) (\(25\%\) số điểm): \(n≤10^{12}.\)

Example

12345(15)12345

618

Mọi thứ nào đó luôn tồn tại \(2\) mặt đối lập nhau. Đó là \(2\) mặt “sự thích” và “sự ghét”. Dù Tấn và Trinh ghét cực ghét những cảnh máu đổ trong Squid Game, nhưng Tấn và Trinh thích Squid Game ở chỗ: Những trò chơi đó đã được nâng cấp từ những trò chơi dân gian Hàn Quốc rất đỗi bình thường. Thế là \(2\) bạn lại lôi cái bàn cờ vua \(n * n\) của Tấn ra (\(n\le 1000\)), mỗi ô được đánh số là \(i\) có tọa độ (\(x_i,y_i\)) thay vì chỉ bằng phẳng thì được chồng lên ai hộp lập phương có cùng kích thước với kích thước ô (\(a_i>0\)):

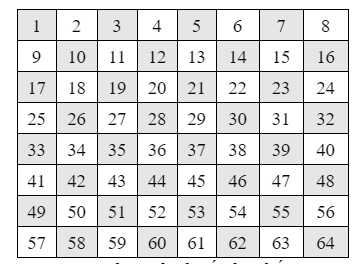
Các ô được đánh số như thế này trong bàn cờ 8x8.

Chơi với cái bàn cờ “kì dị” này riết cũng chán, Tấn đem con Robot nhỏ siêu hiện đại ở nhà ra. Nó hiện đang có 300V trong cái hộp pin siêu cấp của mình và nó cứ mỗi giây chỉ tiêu tốn 0,00001V nếu di chuyển. Tấn đặt nó trên ô số \(1\) và đưa ra một số \(T\), yêu cầu rằng Trinh phải điều khiển Robot đến ô có số \(n^2\) trong thời gian không quá T giây. Biết:

• Robot chỉ có thể di chuyển đến ô lân cận ở bên phải, bên dưới và ô có góc phải dưới, không thể di chuyển đến các ô lân cận khác.
• Tấn muốn ô nào Trinh có thể đi chéo thi hãy đi chéo, không được đi khác đi.
• Robot di chuyển đến ô lân cận ở bên phải, bên dưới và ô có góc phải dưới tốn [1s*((chênh lệch chiều cao giữa 2 ô) +1)] (nếu ô đó cao hơn hoặc bằng phẳng với ô đang đứng, tức là leo lên ô bên cạnh).
• Robot di chuyển đến ô lân cận ở bên phải, bên dưới và ô có góc phải dưới tốn [1s+0,01s*(chênh lệch chiều cao giữa 2 ô)] (nếu ô đó thấp hơn ô đang đứng, tức là rớt xuống ô bên cạnh).
• Robot rất bền để có thể chịu được bất kì chấn động nào (có lẽ trừ động đất). Nhưng yên tâm đi, nhà Tấn không bao giờ có động đất đâu :)))))

VD:

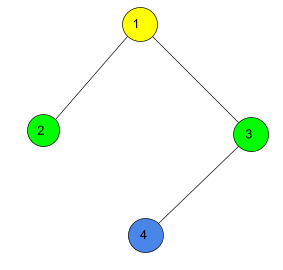
Trong hình này, ví dụ như Robot đang đứng ở ô viền đỏ có màu xanh (có số 2):

• Nếu Robot đi sang ô màu xanh (cũng có số \(2\)) phía dưới thi sẽ tốn \(1s\) di chuyển qua.
• Nếu Robot đi sang ô màu vàng (có số \(1\)) bên phải thì sẽ tốn \(1s + 0.01s = 1.01s\) vì ô vàng có độ cao thấp hơn ô đang đứng là \(1\).
• Nếu Robot đi sang ô màu cam (có số \(3\)) ở bên phải và phía dưới thì sẽ tốn \(1s + 1s = 2s\) vì ô cam có độ cao cao hơn ô đang đứng là \(1\).

Trinh đang đau đầu vì … chỉ đơn giản là đang ăn sáng nên không có thời gian chơi trò này :))). các bạn hãy giúp Trinh biết rằng: Nếu có thể hướng Robot đến ô có số \(n^2\) thì hãy in ra thứ tự của các ô cần di chuyển (kể cả ô kết thúc và ô bắt đầu) tối ưu nhất, còn không hãy in ra từ “Can’t solve”.

Input

• Dòng \(1\) gồm \(2\) số là \(n\) và \(T\);
• \(n\) dòng tiếp theo, mỗi dòng gồm có \(n\) số nguyên \(a\).

Output

• Ghi ra lộ trình đi của Robot, giữa 2 chỉ số có 1 dấu '->' hoặc chữ “Can’t solve”

Scoring

Gọi \(maxA\) là giá trị lớn nhất mảng \(A\), \(minA\) là giá trị nhỏ nhất mảng \(A\), ta có:

• \(maxA, minA\le 10^9;\)
• 30% số test có \(n\le 100, maxA-minA\le 5, T\le 10^3;\)
• 50% số test có \(n\le 200, maxA-minA\le 10, T\le 10^6;\)
• 80% số test có \(n\le 500, maxA-minA\le 500, T\le 10^9;\)
• 100% số test có \(n\le 1000,maxA-minA\le 5000, T\le 10^{12}.\)

Example

3 4
3 2 9
1 3 3
5 2 3 

1 -> 5 -> 9

3 1
3 2 9
1 3 3
5 2 3

Can't solve

Loki hay Thần lừa lọc là em trai khác cha khác mẹ của Thor, là một trong những vị thần ngoại tộc của xứ Asgard. Hiện nay hắn đang làm quản lí tại Cơ quan Quản lý Phương sai Thời gian (TVA), thế chỗ cho He who remains. Sau khi He who remains cưỡi hạc qui tiên, các sự kiện nexus xảy ra không thể kiếm soát; dẫn đến trong Đa vũ trụ xuất hiện n vũ trụ mới, Loki đánh số các vũ trụ này từ \(1\) đến \(n\) theo vị trí xuất hiện mà hắn nhìn thấy.

Công nghệ của các vũ trụ này cực kì phát triển, tới nỗi có một số cặp vũ trụ có thể liên hệ với nhau; mối liên hệ giữa hai vũ trụ là hai chiều, có nghĩa là nếu vũ trụ \(i\) có thể kết nối tới vũ trụ \(j\) thì người ở vũ trụ \(j\) cũng có thể gửi lời hồi âm tới vũ trụ \(i\). Mỗi vũ trụ có một chỉ số đặc trưng \(a_i\) được tính bằng số vũ trụ \(j (j < i)\) sao cho hai vũ trụ \(i\) và \(j\) có thể liên hệ với nhau. Dễ nhận thấy mỗi khả năng các vũ trụ liên kết với nhau sẽ chỉ cho ra duy nhất một dãy đặc trưng, song có thể có nhiều trường hợp các vũ trụ liên kết khác nhau có cùng dãy đặc trưng.

Lo sợ liên minh các vũ trụ quá hùng mạnh, và cũng để giữ sự bình ổn của Đa vũ trụ; Loki muốn xóa đi một số vũ trụ và giữ lại một số liên tiếp nhau các vũ trụ có dãy đặc trưng là \(f\) thỏa mãn:

• Tồn tại ít nhất một khả năng các vũ trụ liên kết nhau có dãy đặc trưng là \(f\)
• Trong tất cả các khả năng các vũ trụ liên kết với nhau nhận \(f\) làm dãy đặc trưng, mỗi vũ trụ có thể kết nối với không quá \(d\) vũ trụ khác

Yêu cầu:

• Cho số nguyên \(d\) và dãy đặc trưng \(a\) của \(n\) vũ trụ mới tạo ra; bạn hãy đếm số cách chọn các vũ trụ liên tiếp nhau có dãy đặc trưng thỏa mãn điều kiện trên, hay nói cách khác bạn hãy đếm số cặp \((L, R) (1 ≤ L ≤ R ≤ n)\) thỏa mãn \(a[L ... R]\) lập thành một dãy đặc trưng thỏa mãn. Hai cặp số gọi là khác nhau nếu có ít nhất một trong hai số tương ứng khác nhau

Input:

• Dòng đầu tiên chứa hai số nguyên dương \(n, d (0 ≤ d ≤ n ≤ 10^5)\)
• Dòng thứ hai chứa \(n\) số nguyên, số thứ \(i\) có giá trị \(a_i (1 ≤ i ≤ n, 0 ≤ a_i ≤ i − 1)\)

Output:

• Xuất ra một số nguyên duy nhất là số cặp số \((L, R)\) thỏa mãn

Scoring:

• Có 25% số test ứng với 25% số điểm của bài toán có \(n ≤ 200\)
• Có 25% số test ứng với 25% số điểm của bài toán có \(n ≤ 2000\)
• Có 25% số test ứng với 25% số điểm của bài toán có \(n ≤ 10^5, a_i ≥ d − 10 ∀i: 1 ≤ i ≤ n\)
• Có 25% số test ứng với 25% số điểm của bài toán có \(n ≤ 10^5\)

Example

LQDOJ có \(n\) problem-setter, được đánh số từ \(1\) đến \(n\); có \(m\) tag bài tập trên hệ thống, mỗi người trong \(n\) nhân vật trên đều có một số sở trường bài riêng (như DP, Đồ thị, ...). Hệ thống LQDOJ cũng có một cách phân cấp quản lí các Problem-setter, trong đó người \(x\) có quyền quản lí người \(i\) nếu và chỉ nếu một trong hai điều kiện sau xảy ra:

• Người \(x\) được phân công trực tiếp quản lí người \(i\)
• Người \(x\) có quyền quản lí người \(z\) mà người \(z\) được phân công trực tiếp quản lí người \(i\)

Người mang số \(1\) có quyền quản lí cấp cao nhất và chỉ dưới quyền của Admin Small

Nhân dịp LTPQ giải Nhất VOI và DXMH đạt được cú ăn ba lịch sử, thầy Small yêu cầu \(n\) người tổ chức các contest cho các bạn thí sinh của LQDOJ làm; mỗi người có thể nhờ những người mình quản lí chuẩn bị bài giúp theo các sở trường của họ, mỗi người chỉ ra bài đúng theo sở trường của mình.

Chú ý: Một người có thể ra nhiều bài

Yêu cầu: Với mỗi người, tính số loại bài phân biệt có thể xuất hiện trong contest của người đó; biết mỗi người khi được quản lí của mình nhờ làm bài thì sẽ không bao giờ từ chối

Input

• Dòng đầu tiên chứa hai số nguyên \(n, m (1≤n,m/3≤10^6)\) lần lượt là số Problem-setter và số tag bài có trên LQDOJ
• Dòng thứ \(i\) trong số \(n\) dòng tiếp chứa số nguyên dương \(t_i\) là số loại bài sở trường của người thứ \(i\), theo sau đó là \(t_i\) số nguyên dương phân biệt mô tả các dạng bài sở trường của người \(i\)
• Dòng thứ \(n+2\) chứa \(n−1\) số nguyên \(p_2, p_3, ... , p_n\) \((1≤p_i≤i), p_i\) là người được phân quản lí trực tiếp người \(i\).

Output

• Một dòng duy nhất chứa \(n\) số nguyên là số bài tối đa có thể xuất hiện trong contest của mỗi người

Example

4 3
1 1
2 1 2
1 2
1 3
1 1 3

3 2 2 1

Scoring

Trong mọi test có: \(t_1 + t_2 + ... + t_n <= 10^7\)

• Subtask \(1\): 50% số test ứng với 50% số điểm của bài có \(n, m ≤ 1000\)
• Subtask \(2\): 35% số test ứng với 35% số điểm của bài có \(n ≤ 10^5\)
• Subtask \(3\): 15% số test ứng với 15% số điểm còn lại có \(n ≤ 10^6\)

Tấn là một người theo chủ nghĩa không hoàn hảo. Anh rất ghét những thứ hoàn hảo, số hoàn hảo cũng không phải ngoại lệ.

Một số \(x\) nguyên dương được gọi là số hoàn hảo, khi:

Trọng đó, \(s(x)\) là hàm tổng các ước của \(x\), không bao gồm \(x\).

Một hôm, anh gặp bài tập về dãy số như sau:

Xét dãy \(a\) gồm \(n\) số nguyên, ban đầu đều là \(0\), thực hiện \(q\) truy vấn thuộc \(2\) loại sau trên dãy \(a\):

• \(1\) \(l\) \(r\) \(v\) : \(a_i = v (1 \le l \le i \le r \le n, 0 \le v \le 10^9)\).
• \(2\) \(l\) \(r\) \(v\) : \(a_i = a_i + v (1 \le l \le i \le r \le n, 0 \le v \le 10^9)\).

Sau khi thực hiện \(q\) truy vấn thì in ra mảng \(a\).

Tuy nhiên có một vấn đề : Vì Tấn không thích số hoàn hảo, nên dãy \(a\) không được có sự xuất hiện của số hoàn hảo. Vậy nên khi thực hiện truy vấn \(i\), nếu trong dãy có số hoàn hảo xuất hiện, thực hiện tăng các số có vị trí từ \(l_i . . . r_i\) của dãy \(a\) lên \(1\) liên tục cho đến khi dãy không còn số hoàn hảo nào.

Tuy nhiên việc này vô tình khiến bài toán trở nên khó hơn rất nhiều. Hơn nữa Tấn đang cần học bài để thi kiểm tra trên lớp. Các bạn hãy giúp Tấn giải bài toán nhé.

Input

• Dòng đầu nhập 2 số \(n\) và \(q\) lần lượt là số phần tử của dãy \(a\) và số truy vấn. \((1 \le n, q \le 10^5)\).
• \(q\) dòng tiếp theo, mỗi dòng nhập vào \(4\) số nguyên dương \(type\) \(l\) \(r\) \(v\) \((1 \le type \le 2)\).

Output

• In ra mảng sau khi thực hiện \(q\) truy vấn.

Scoring

• Subtask \(1\) (40% số điểm): \(n, q \le 10^3\)
• Subtask \(2\) (60% số điểm): Không có ràng buộc gì thêm

Example

5 7
2 1 5 1 
2 2 5 1 
2 3 5 1 
2 4 5 1 
2 5 5 1 
2 3 5 1 
1 1 3 28 

29 29 29 8 9